Portal about sewerage and downpipes / Septic tanks / The scope of functions in the tasks of the exam. Solving typical problems Find a set of function values on an interval

The scope of functions in the tasks of the exam. Solving typical problems Find a set of function values on an interval

25.12.2021

Function y=f(x) is such a dependence of the variable y on the variable x when each valid value of the variable x corresponds to a single value of the variable y .

Function scope D(f) is the set of all possible values of the variable x .

Function range E(f) is the set of all valid values of the variable y .

Function Graph y=f(x) is the set of plane points whose coordinates satisfy the given functional dependence, that is, points of the form M (x; f(x)) . The graph of a function is a line on a plane.

If b=0 , then the function will take the form y=kx and will be called direct proportionality.

D(f) : x \in R;\enspace E(f) : y \in R

The graph of a linear function is a straight line.

The slope k of the straight line y=kx+b is calculated using the following formula:

k= tg \alpha , where \alpha is the angle of inclination of the straight line to the positive direction of the Ox axis.

1) The function increases monotonically for k > 0 .

For example: y=x+1

2) The function monotonically decreases as k< 0 .

For example: y=-x+1

3) If k=0 , then giving b arbitrary values, we get a family of straight lines parallel to the axis Ox .

For example: y=-1

Inverse proportionality

Inverse proportionality is called a function of the form y=\frac (k)(x), where k is a non-zero real number

D(f) : x \in \left $ R/x \neq 0 \right $; \: E(f) : y \in \left $R/y \neq 0 \right $.

Function Graph y=\frac (k)(x) is a hyperbole.

1) If k > 0, then the graph of the function will be located in the first and third quarters of the coordinate plane.

For instance: y=\frac(1)(x)

2) If k< 0 , то график функции будет располагаться во второй и четвертой координатной плоскости.

For instance: y=-\frac(1)(x)

Power function

Power function is a function of the form y=x^n , where n is a non-zero real number

1) If n=2 , then y=x^2 . D(f) : x \in R; \: E(f) : y \in; main period of the function T=2 \pi

GBOU lyceum (economic) with. Isakla

Mathematics teacher Kuzaeva V.N.

2016

Reference materials

Solution Sample Find set of function values

Function scope
is an

y - any number

Function scope
is an y - any number

Many values

y - any number

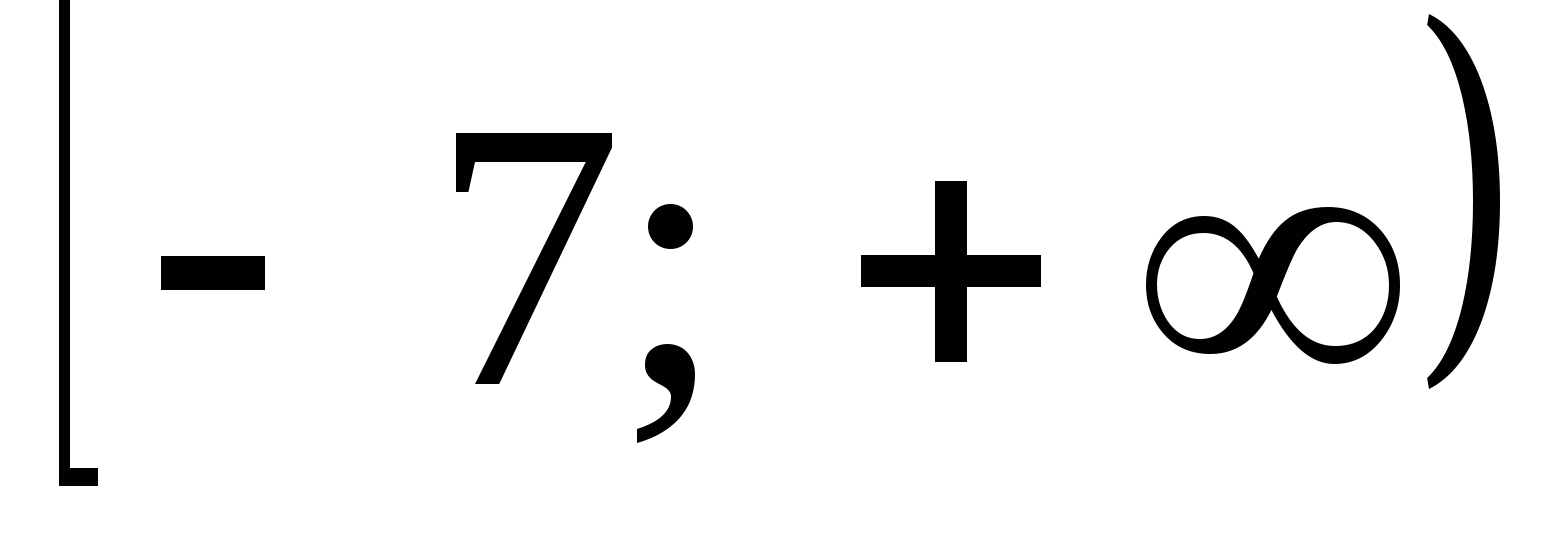
Highest value

Lowest value

Domain X - any number
, where

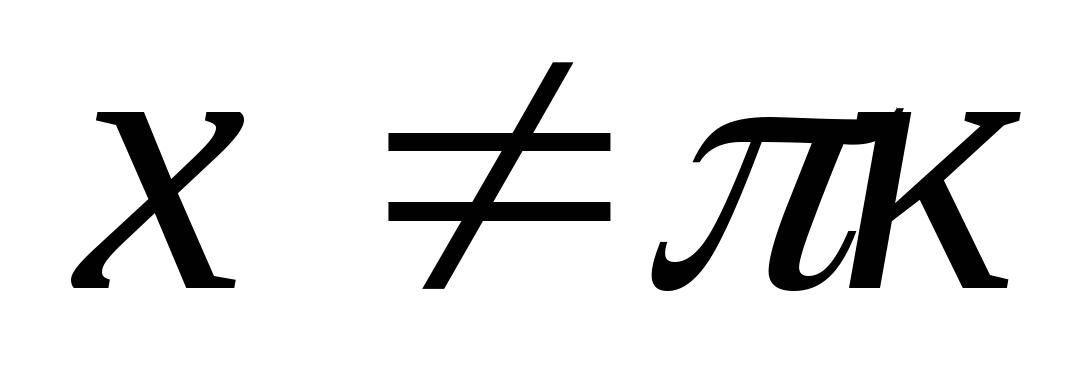, where

Many values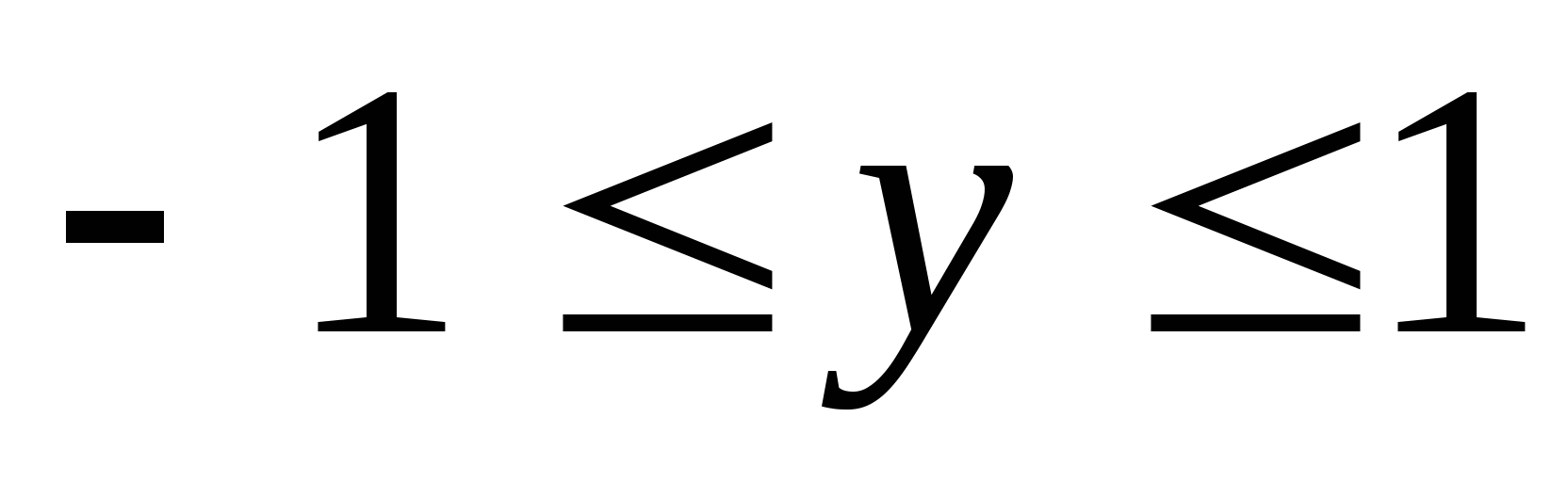
y - any numbery - any number

Plot templates for some trigonometric functions

Set of values of trigonometric functions

Option 1

Y =sin 3x+2.

1) (-5;5) 2) 3) 4) (1;5)

2. Find the area of \u200b\u200bthe function y =tg x + 1.

1) 3) (-∞;∞) 4)

1) -6 2) 6 3) -4 4) -2

4. Specify the smallest integer from the range of the function

y = 12.7 + 5 sin(3x-2).

1) -5 2) 8 3) 5 4) 17

5. Specify the function whose set of values is the segment [-2;2].

1) y = cos 2x 2) y = sin 2 x 3) y = cos 2 x +2

4) y = 2 sin 4 x

6. Find the set of function valuesy = tg 2 xon the segment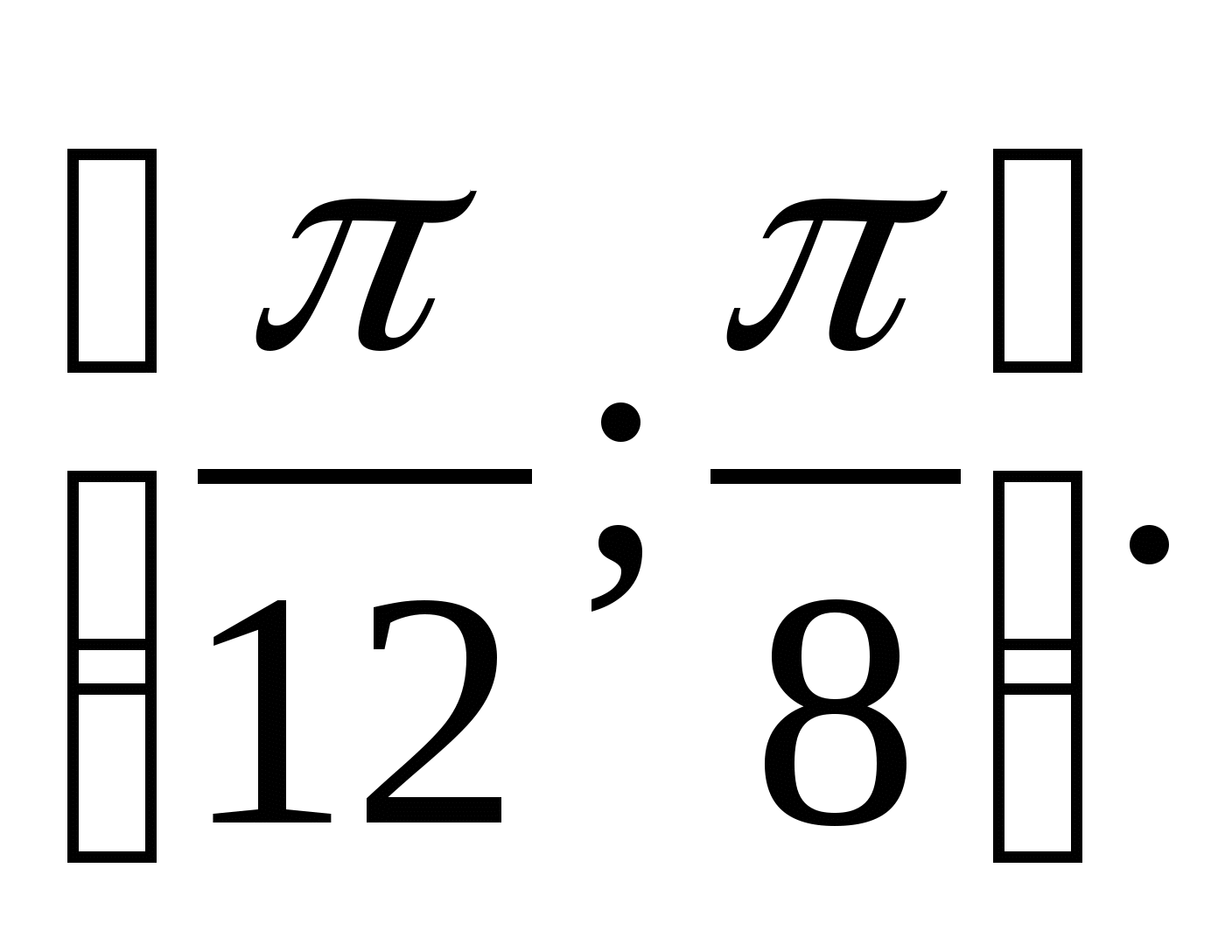

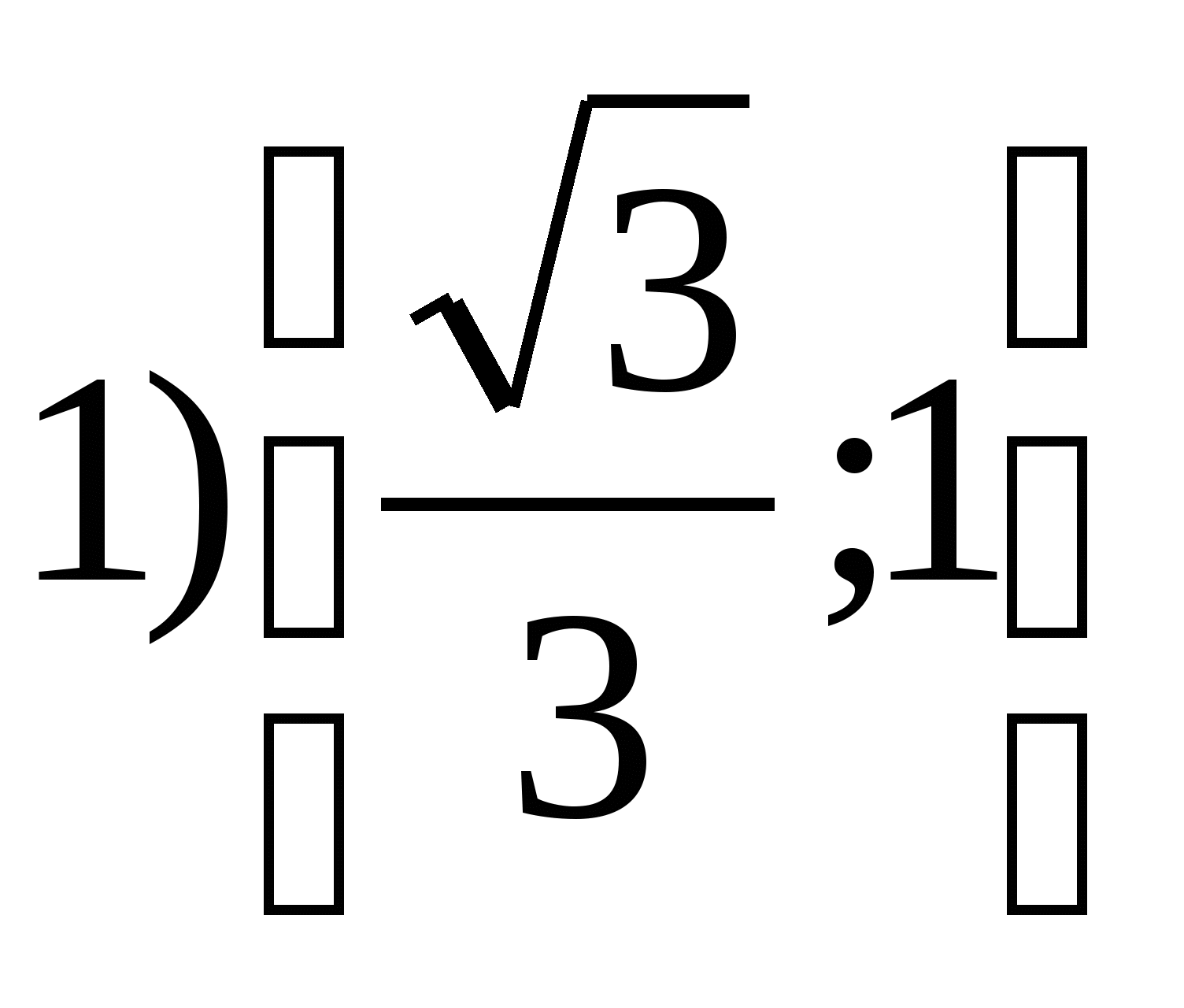
7. Find the sum of all integers that are in the range of the functiony = 4 cos 2 x – 7.

1) -25 2) 25 3) -22 4) 0

Option 2

y = 2 cos 5 x +3.

1) (2;3) 2) 3) (1;5) 4) .

2. Find the scope of the function

1) 3) (-∞;∞) 4) .

3. Specify the smallest number from the range of the function

1) 4 2) -3 3) 1 4) -7

4. Specify the largest integer from the range of the function

1) 2 2) 13 3) 12 4) -2

5. Specify a function whose set of values is the segment [-5;5].

1) y = sin 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = sin 5x + 5

6. Find the set of function values
on the segment

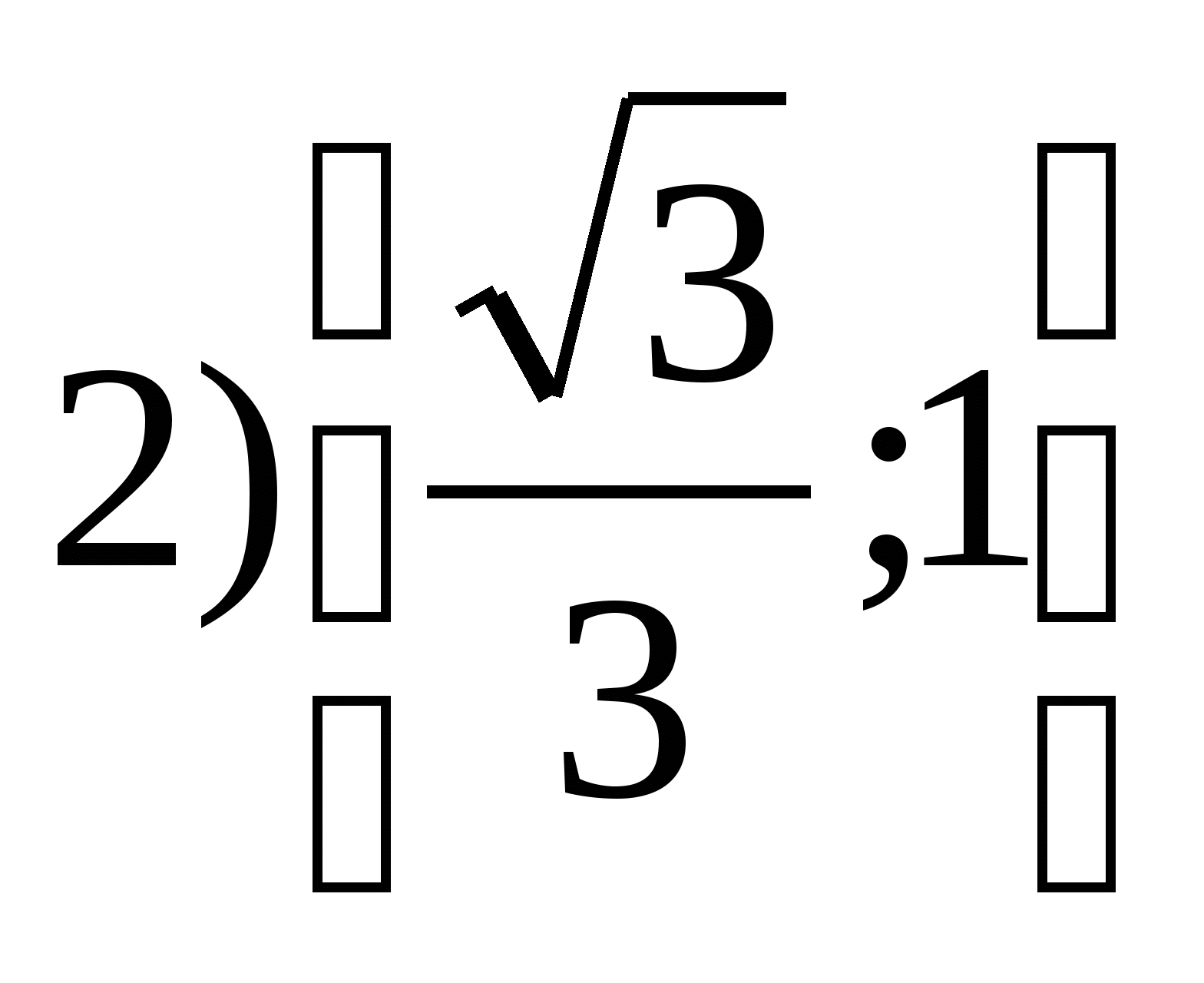
7. Find the product of all integers that are in the range of the function y \u003d 5 - 3sin 2 x.

1) 120 2) 14 3) -15 4) 0

Option 3
1. Specify a set of function valuesy = sin 3 x + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. Specify the smallest number from the range of the function y = 5tg 2 x+2?

1) 5 2) 0 3) 7 4) 2

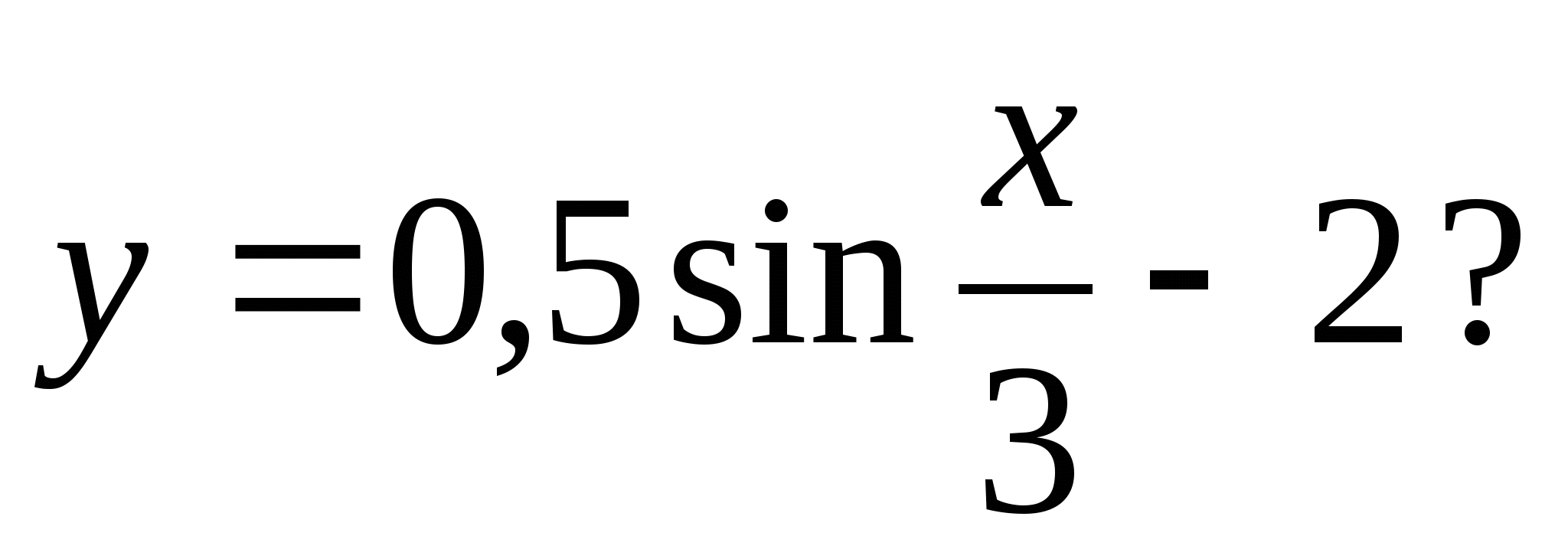
1) -1 2) -2,7 3) -2,3 4)-3

5. Specify a function whose set of values is a segment

[-17;-13].

1) y \u003d 5 sin x - 8 3) y \u003d -cos x +15

2) y = 2 cos x - 15 4) y = 3 sin x +10

6. Indicate the smallest natural number that is not included in the set of function values

1) 2 2) 4 3) 15 4) 6

7. How many integers belong to the set of function values

y = 2 cos 3 x +10?

1) 2 2) 3 3) 4 5) 5

Option 4

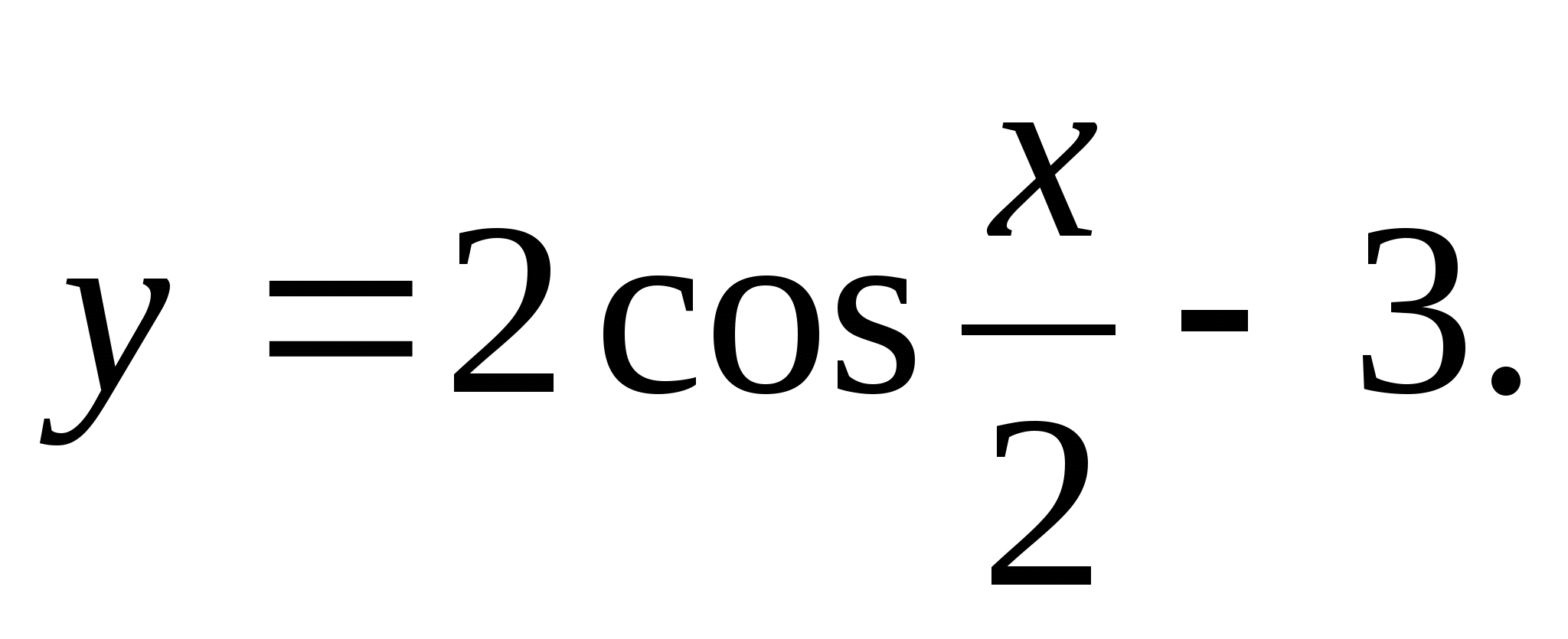
1) 2) 4) (-7;-6)

2. Find the range of the function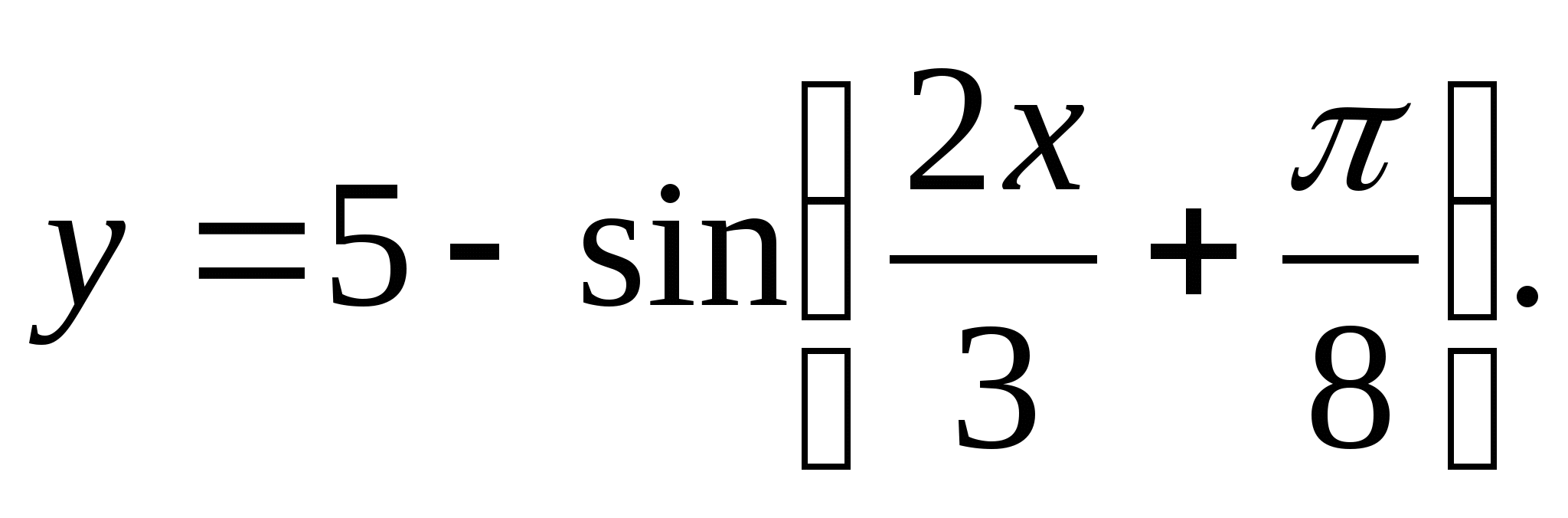

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. Specify the largest number from the range of the functiony = -3 ctg 2 x+7.

1) 10 2) 4 3) 7 4) -3

4. Which of the following numbers is not included in the set of function values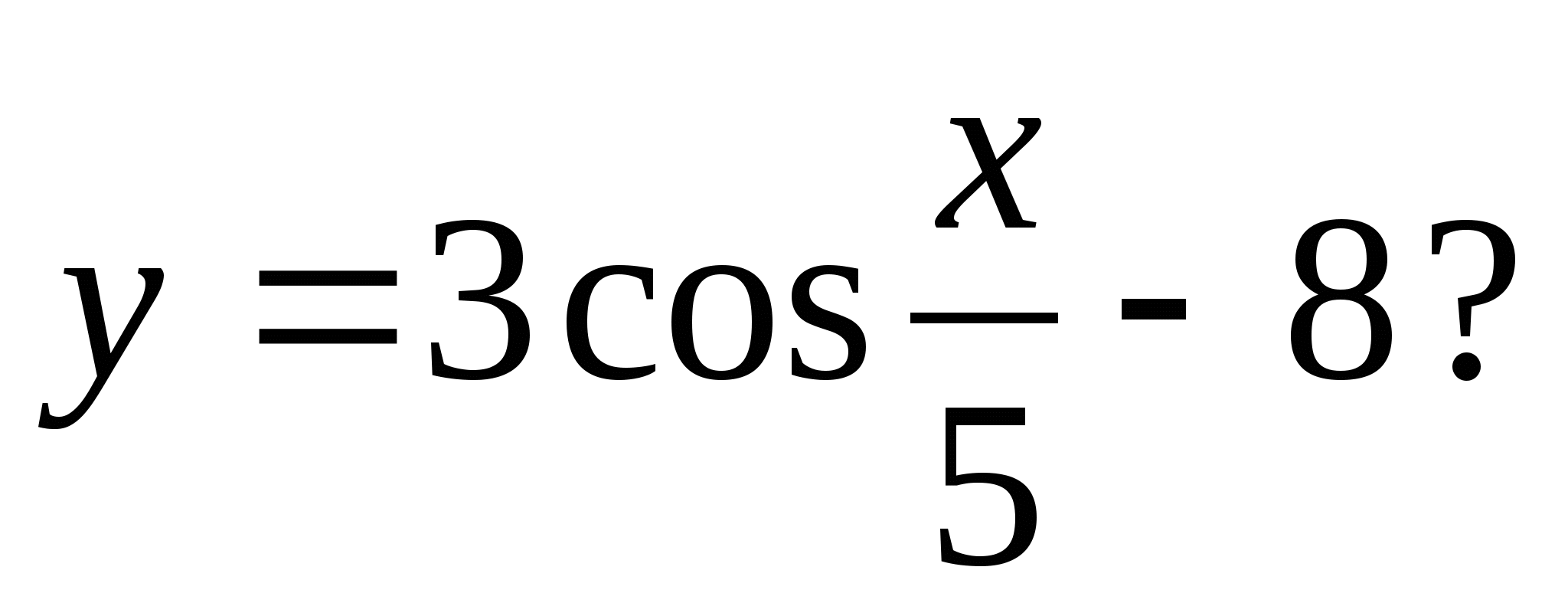

1) -6 2) -5 3) -10 4) -7

5. Specify a function whose set of values is the interval .

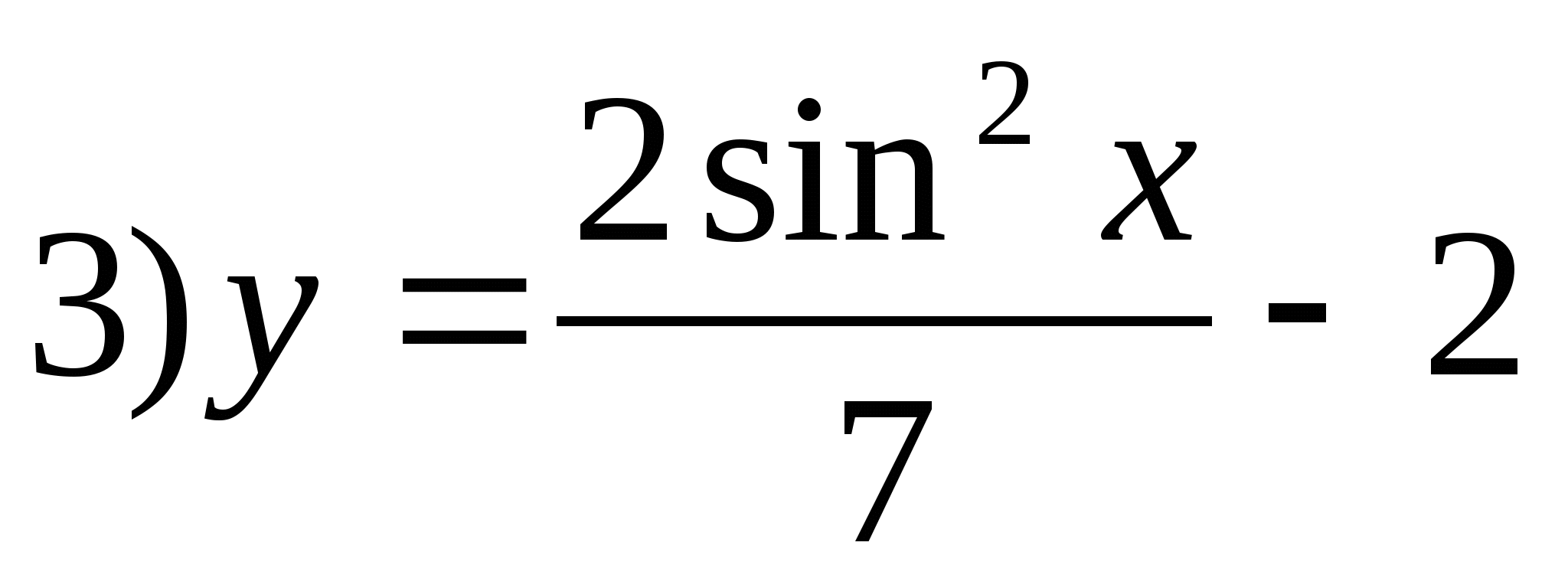
6. Specify the largest negative integer that is not included in the range of the function

1) -1 2) -25 3) -6 4) -2

7. How many integers belong to the set of function values

1) 11 2) 3 3) 5 4) 4

Option 5

1. Specify the set of function values y = 2 -sin 5 x.

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. Find the range of the function

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. Specify the smallest integer from the range of the function

y = 3 + sin 2 2 x.

1) 0 2) 1 3) 3 4) 4

4. Which of the following numbers is included in the set of function values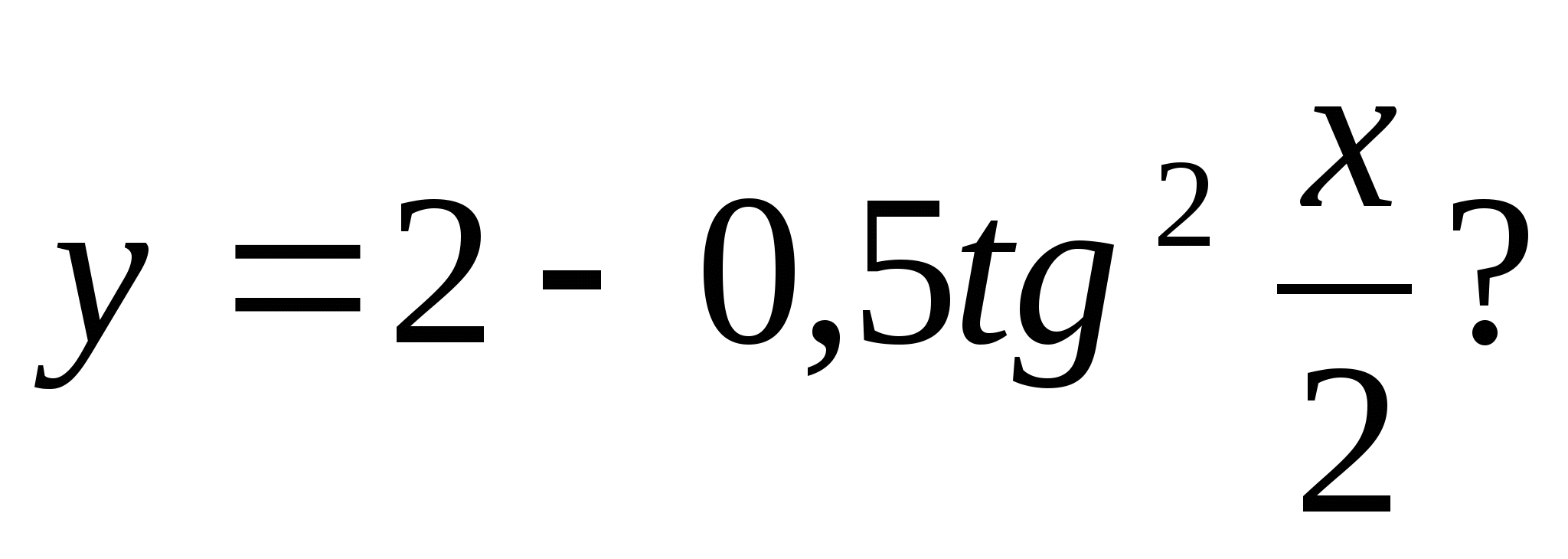

1) 128 2) 10,5 3) 3 4) -235

5. Specify the function whose set of values is the segment [-9;15].

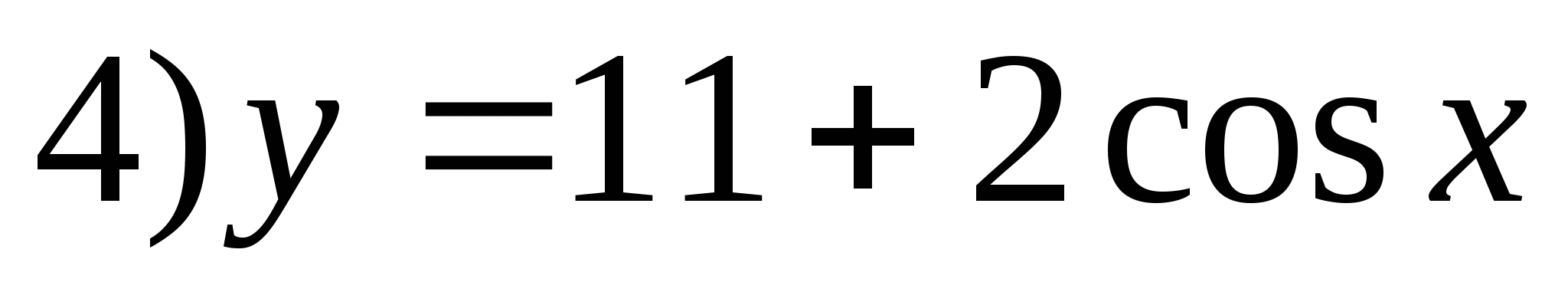
6. Find the sum of integers included in the set of function values

1) 0 2) 7 3) 18 4) 22

7. Find the largest value of a function
on the segment

1) 0,5 2) 1,5 3) 0 4) 2

Option 6

1. Specify the segment corresponding to the set of function values

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. Find the range of the function

3. Specify the largest number from the range of the function

1) 5 2) -6 3) -3 4) 4

4. Which of the following numbers is included in the set of function values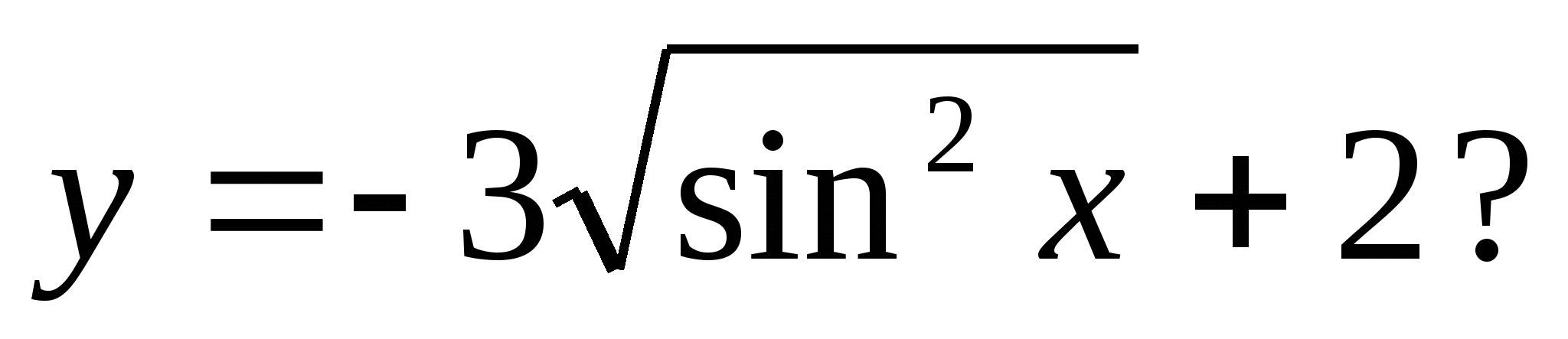

1) 5 2) 0 3) -3 4) 4

5. Specify a function whose set of values is the interval .

1) at = 15 – 7 cos 2x 3) y = 7 cos 2x + 3

2) y = 5 cos 4 x 4) y = - tg 2 x + 1

6. Find the product of integers included in the set of values

y = 3,8 – 1,4 sin 3 x.

1) 17 2) 12 3) 0 4) 60

7. Find the set of function values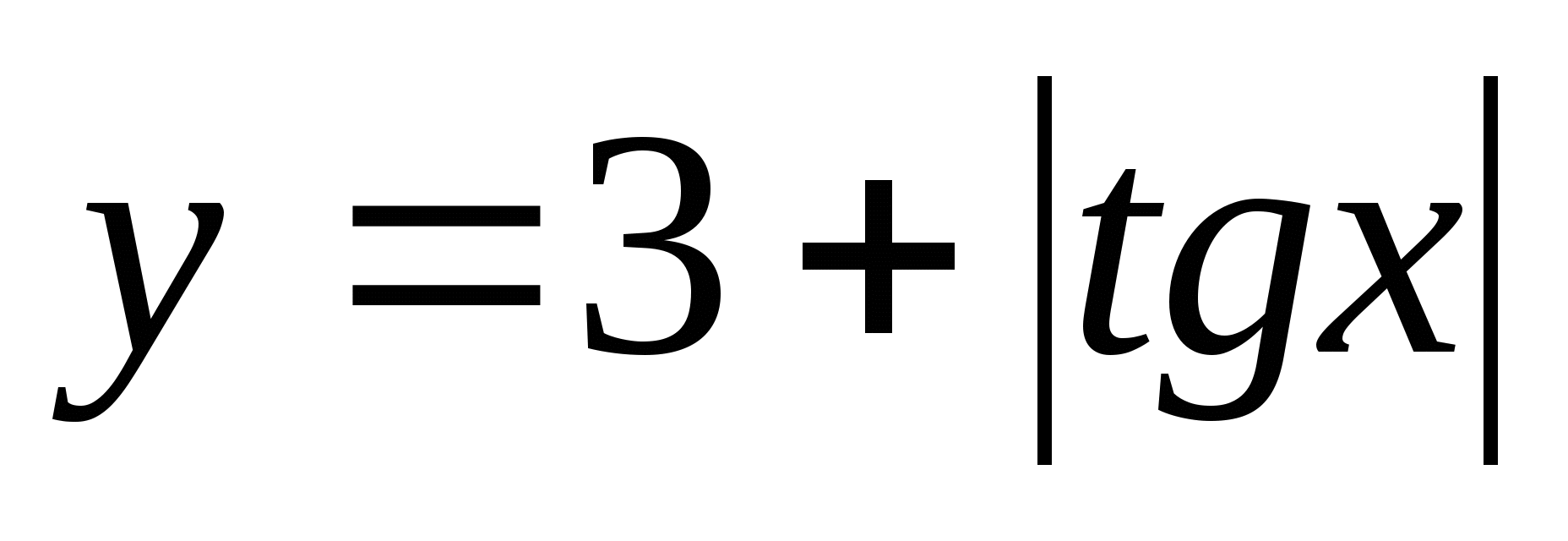
in between

1) (3;4) 2) 3)

Option 7

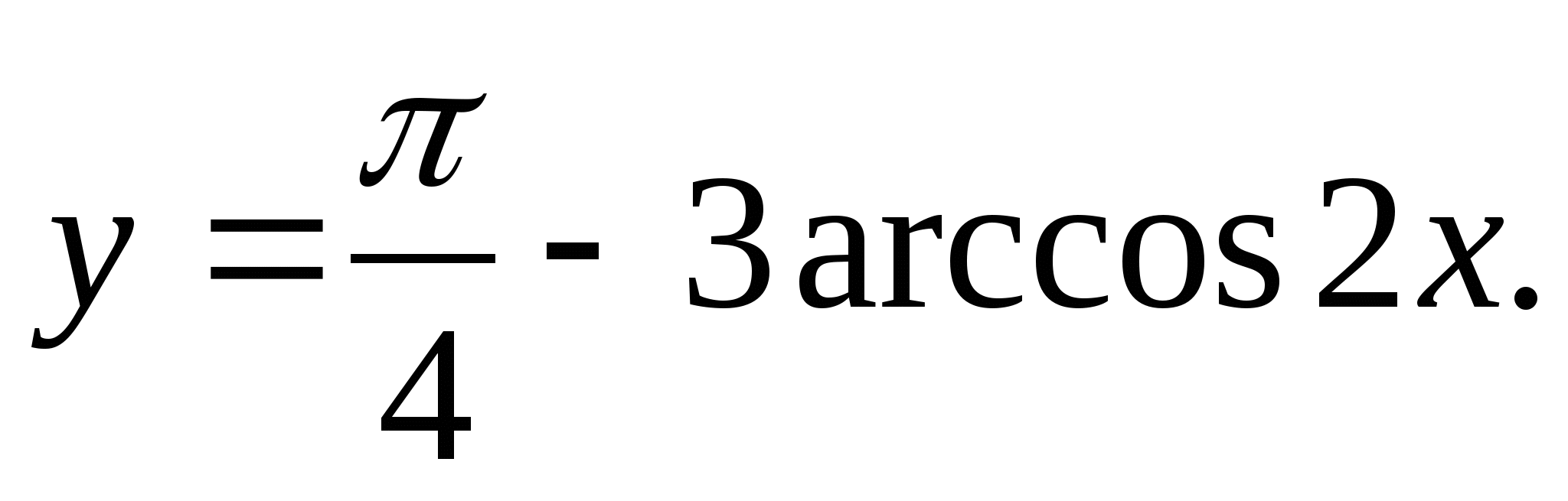
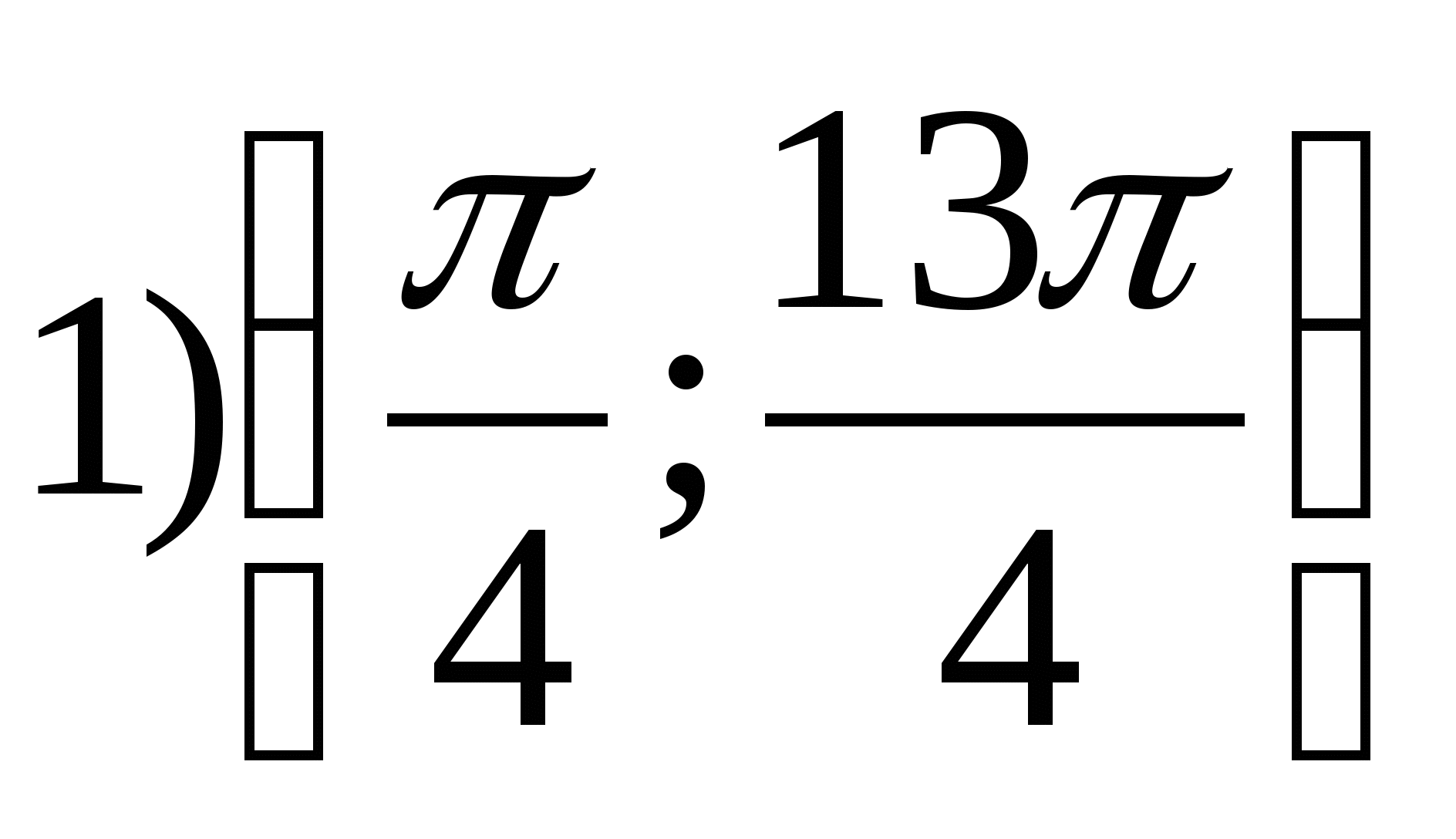
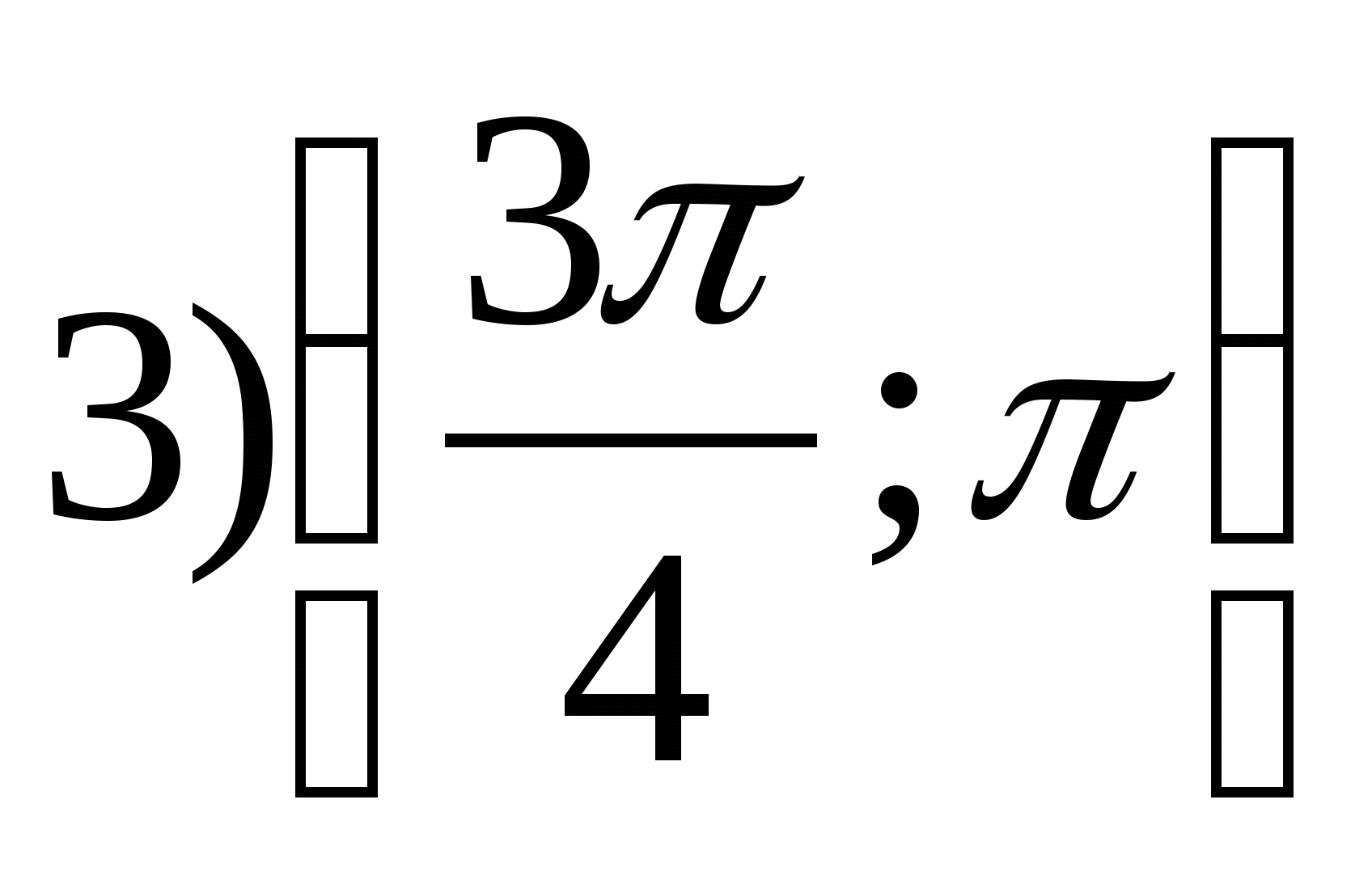
2. Find the smallest integer value of the function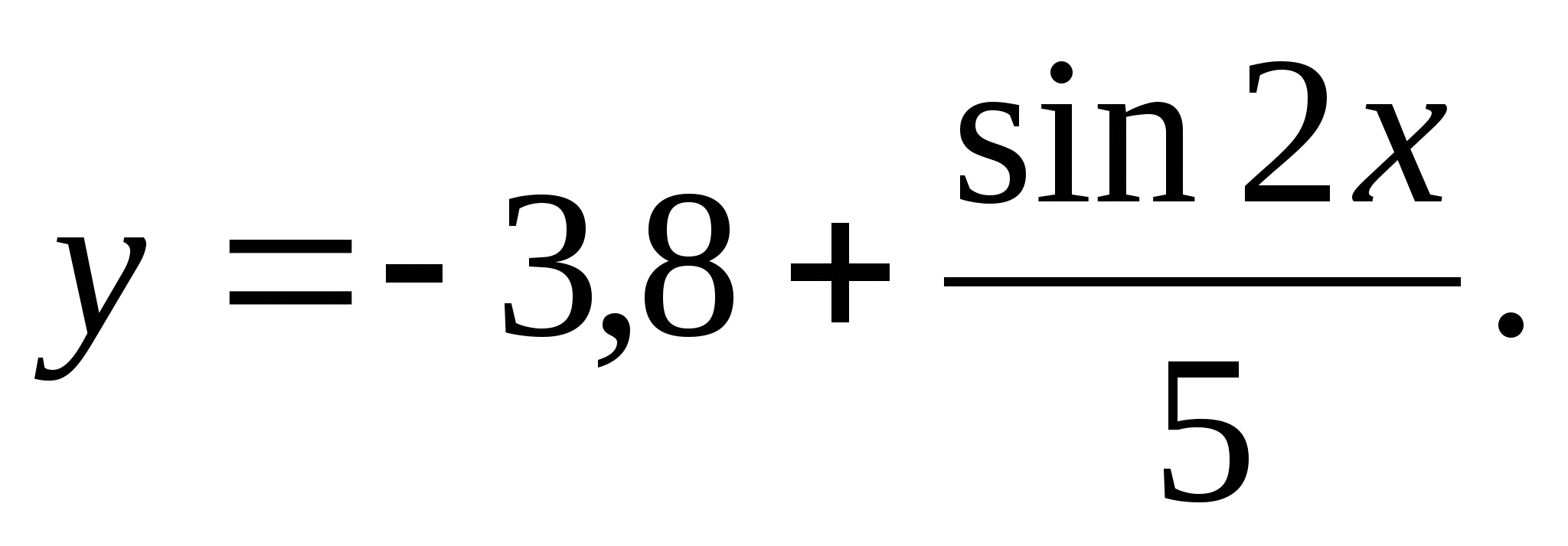

1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6

4. For what values of a does the equationsin(3 x-4)+5= a solvable?

1) 2) 3) (4;6) 4) (-6;4]

sin 2 2 x – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]

in between

2) 0 3) 1

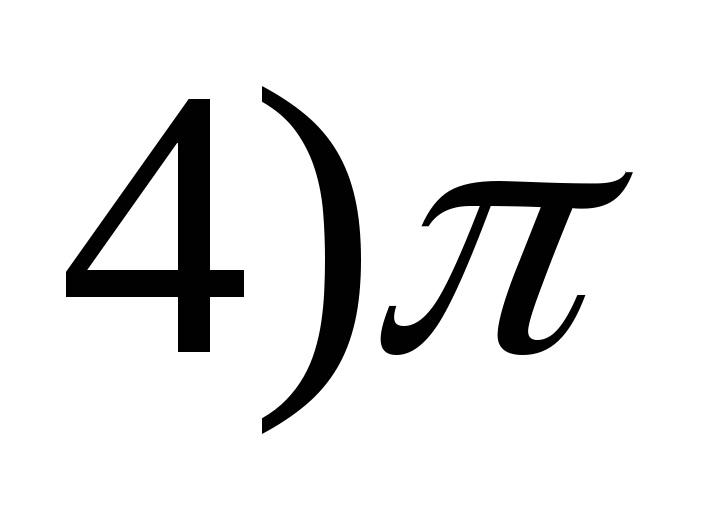
y = 4 sin(x 4 ) -2?

1) 8 2) 9 3) 7 4) 10

Option 8

1. Find the set of function valuesy = arctgx- 2π.

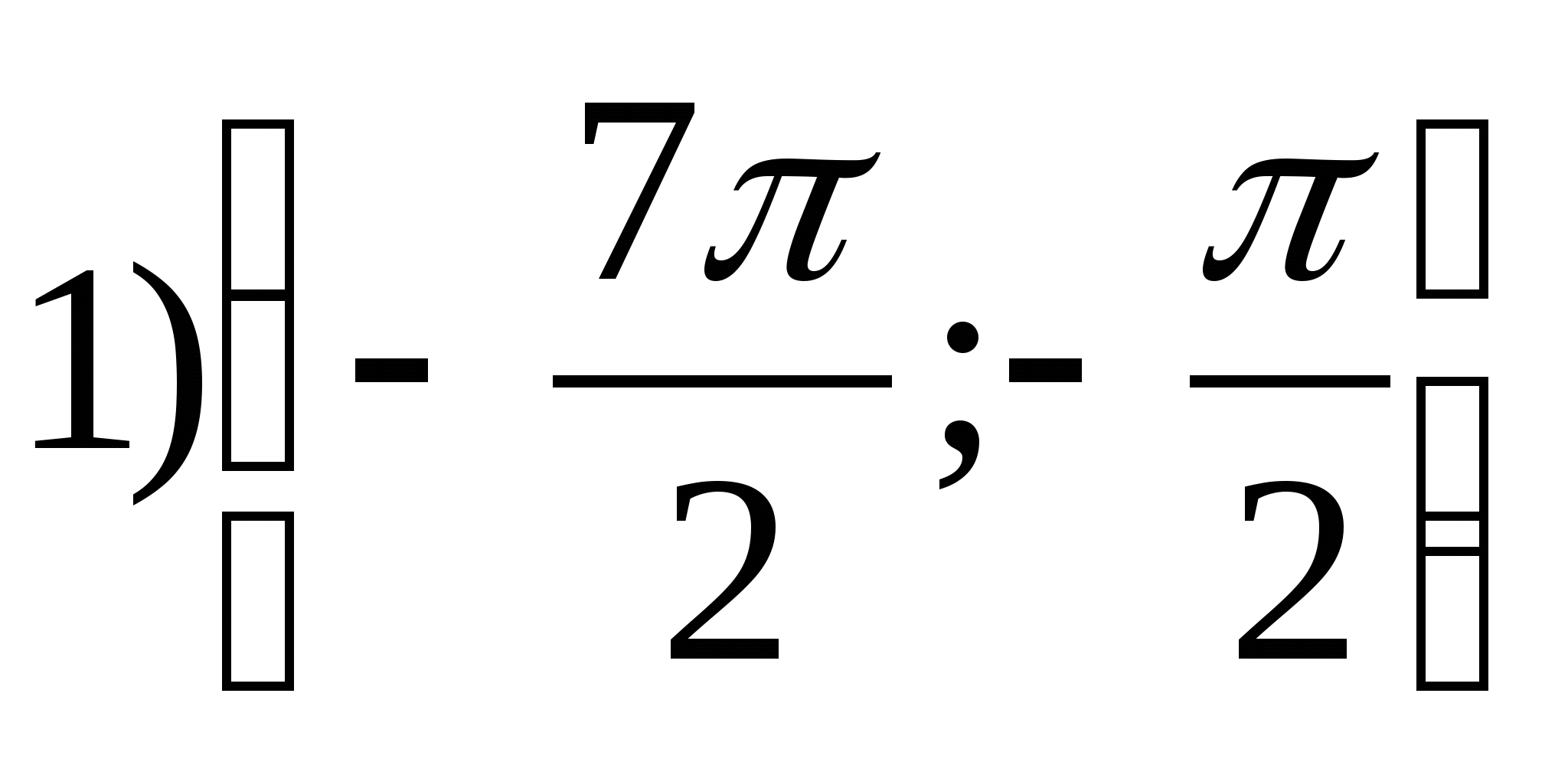
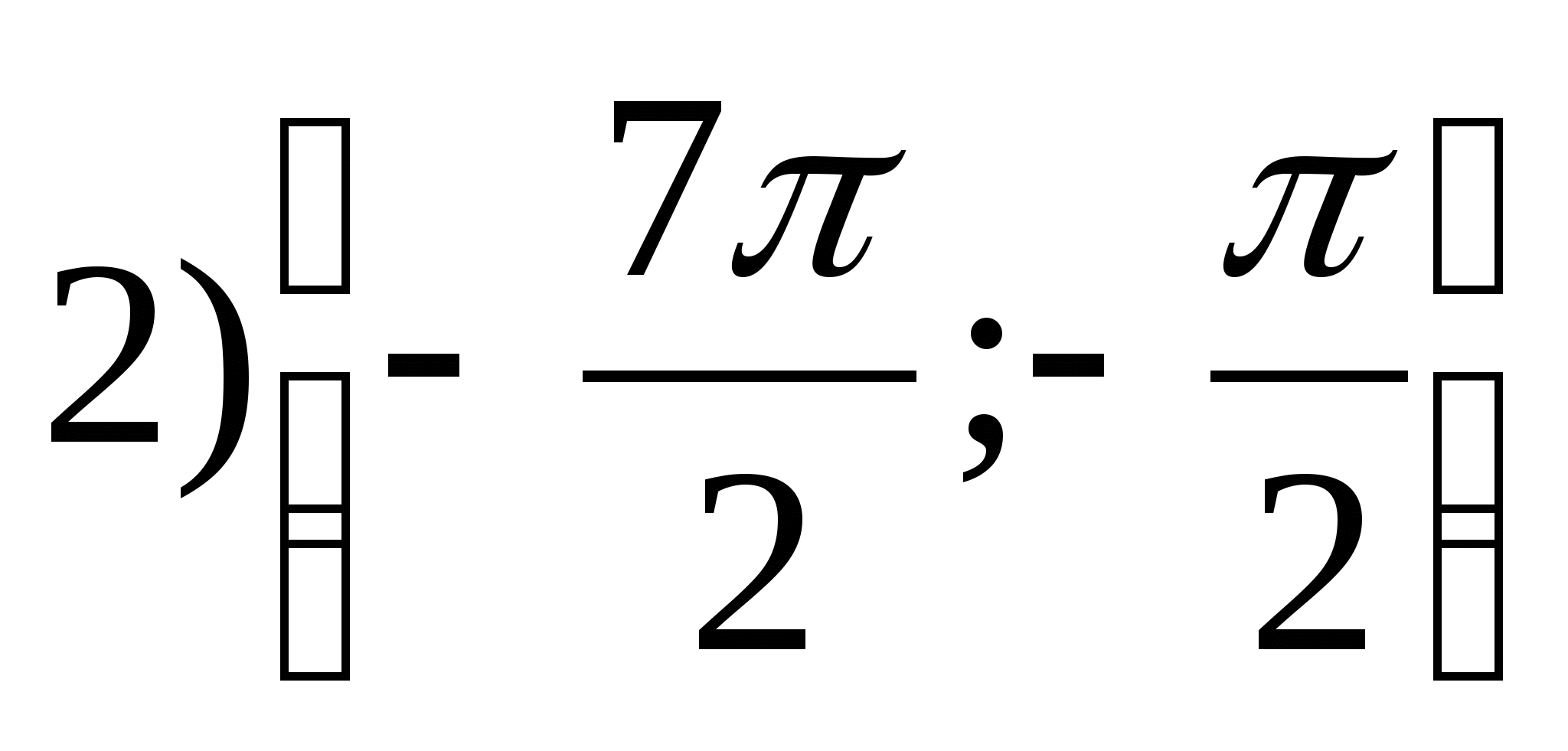
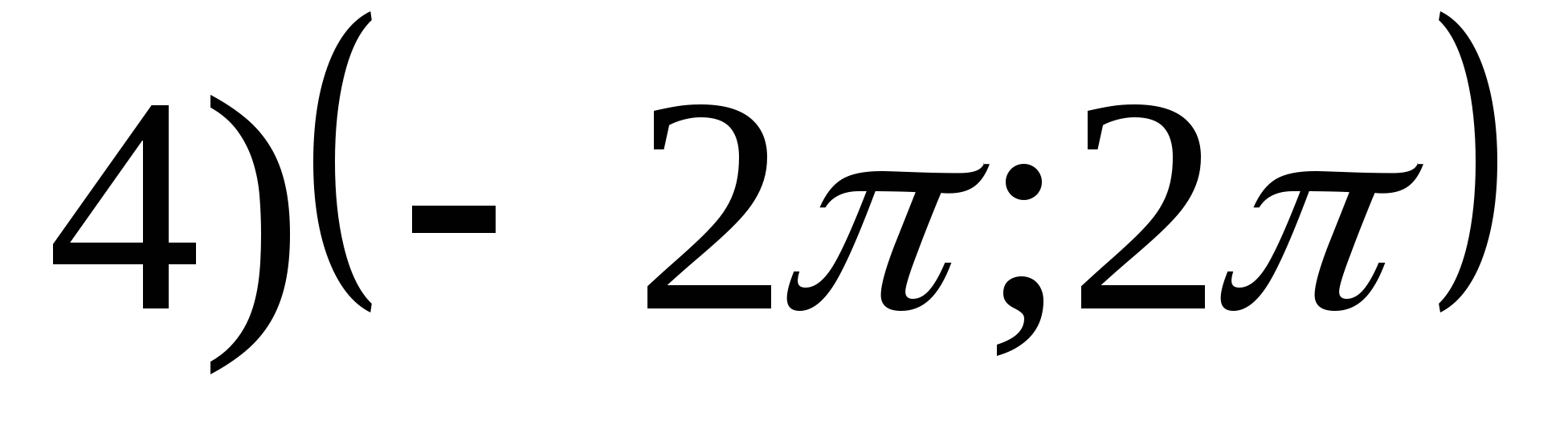
2. Find the largest value of the function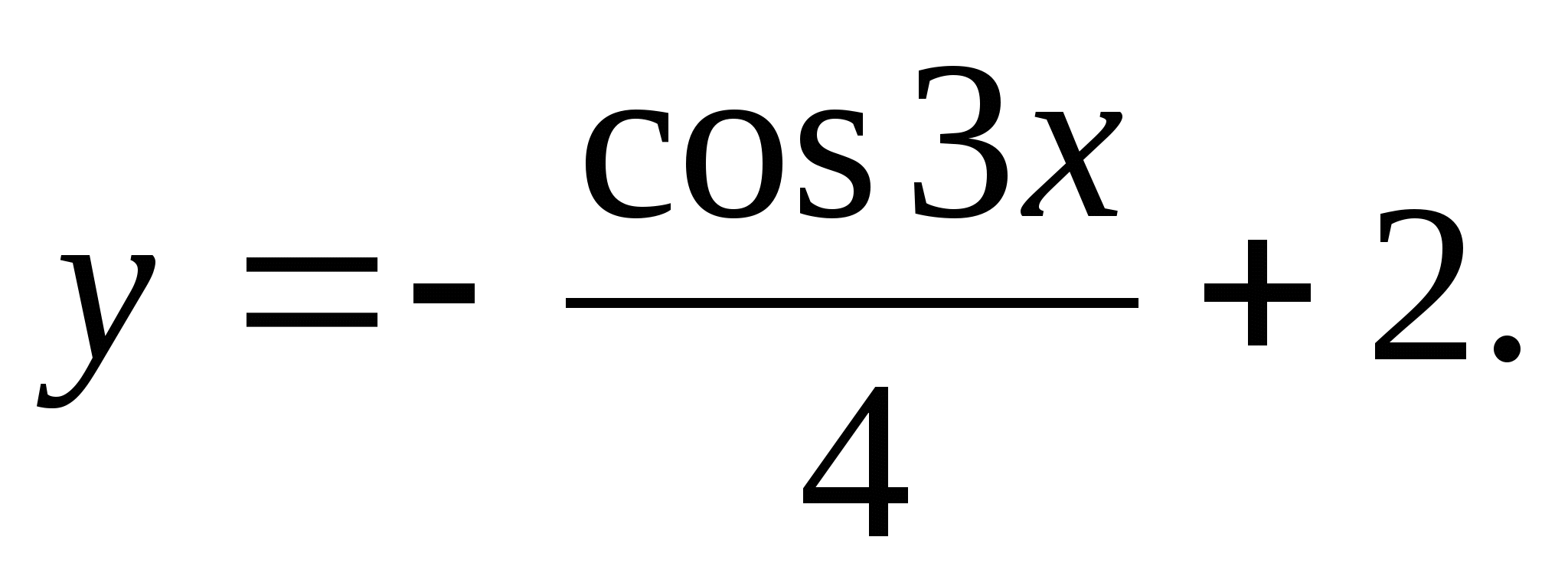

1) 1,75 2) 0 3) 2,25 4) -1,75

3. Which of the following numbers can be the value of the function

1) -4 2) -2 3) 0 4) 2

4. For what values of p equation -2+cos(4 x-1)= p has roots?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. Find the set of function valuesy = -2 tg 2 x + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)

in between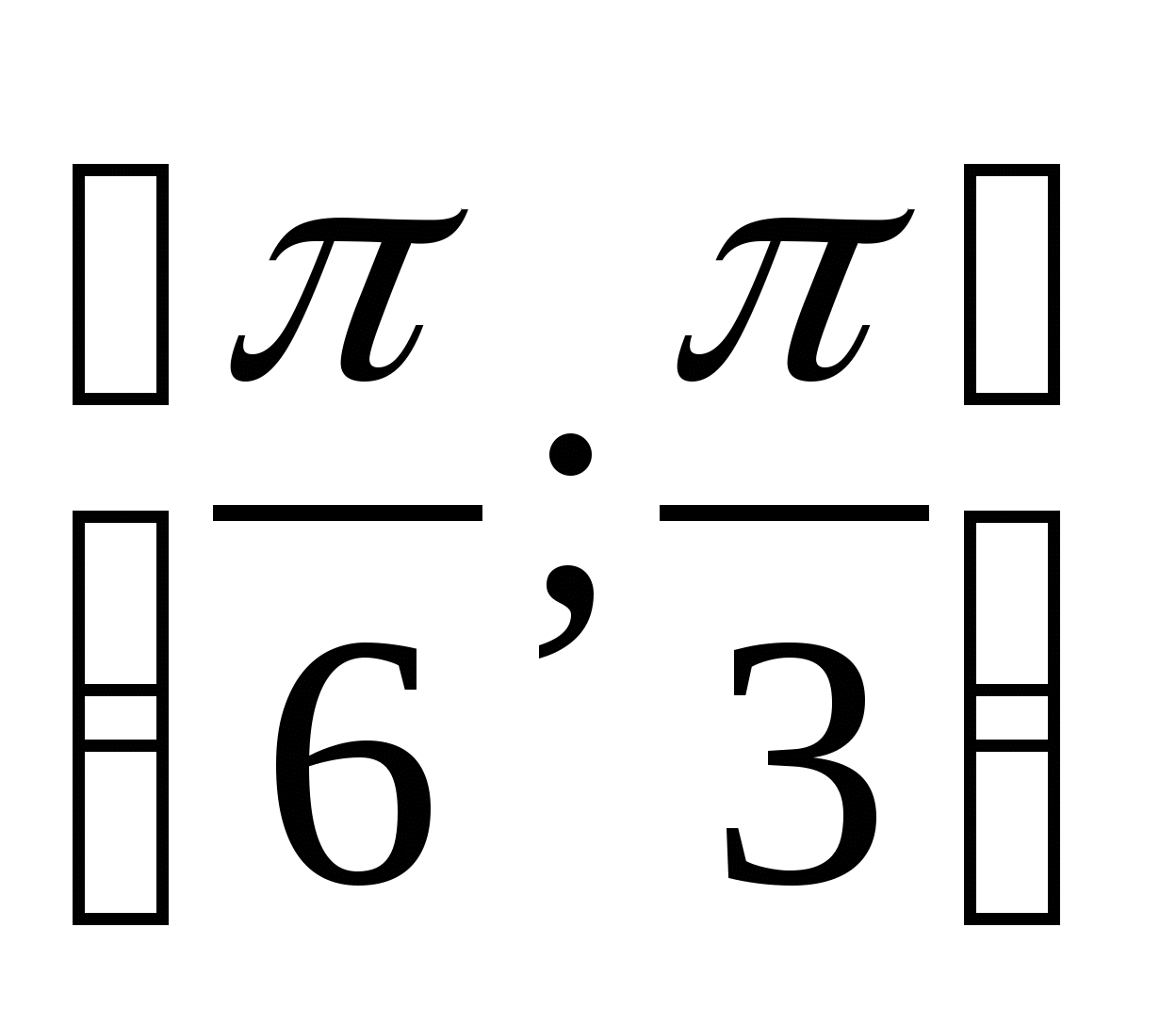
.

1) 0 2) 1 3) -1 4) 3

7. How many integers are in the range of the function

1) 4 2) 3 3) 5 4) 2

Option 9

1. Find the range of the function

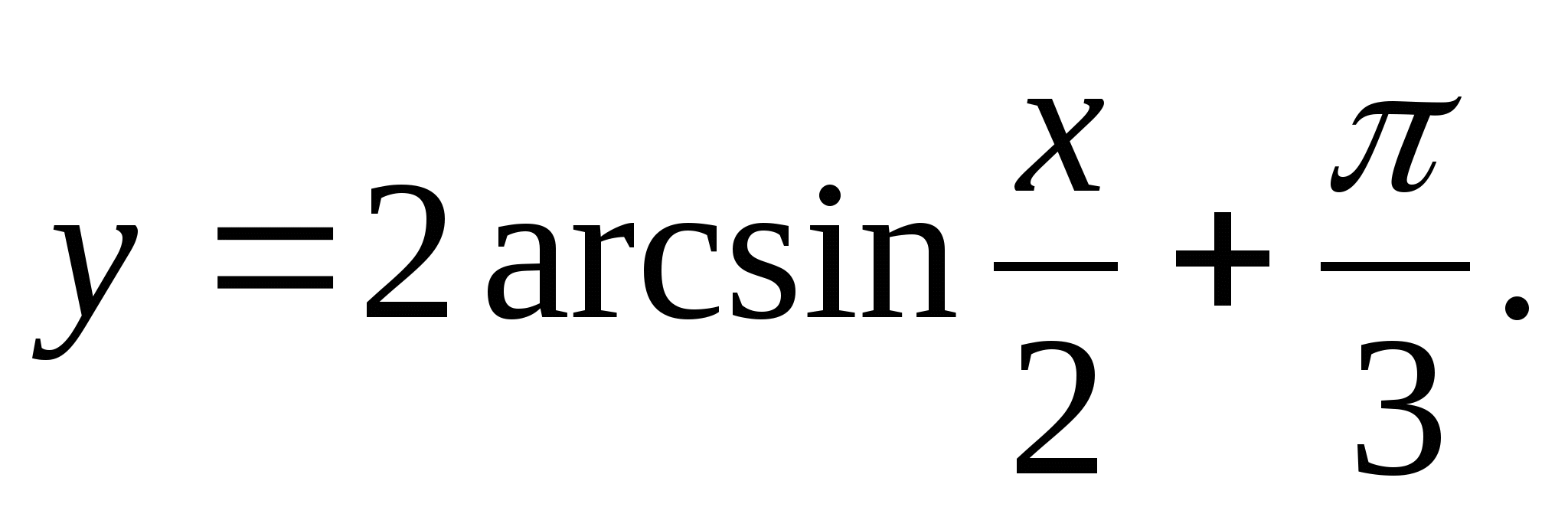
2. Find the largest integer value of the function

1) 4 2) 5 3) 6 4) 7

3. Which of the following numbers can be the value of the function

1) 0 2) 3 3) 6 4) 9

k the equation - k + sin(2 x-1) = 2 solvable?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. Find the set of function values \u200b\u200by \u003d -cos 2 3 x + 4.

1) 2) 3) 4)

6. Specify the smallest value of the function
in between

2) -1 3) 0 4) 1

7. Find how many integers are in the range of the function y = 12cos 3 x +5 sin 3 x.

1) 13 2) 27 3) 26 4) 14

Option 10

1. Find the range of the function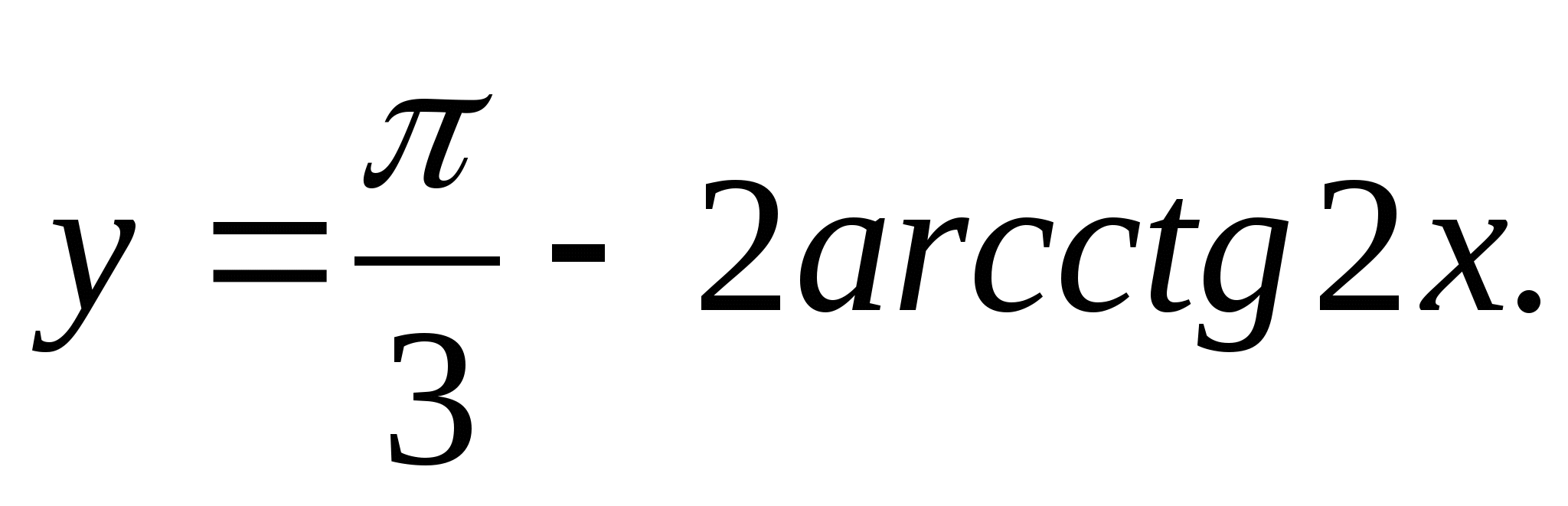

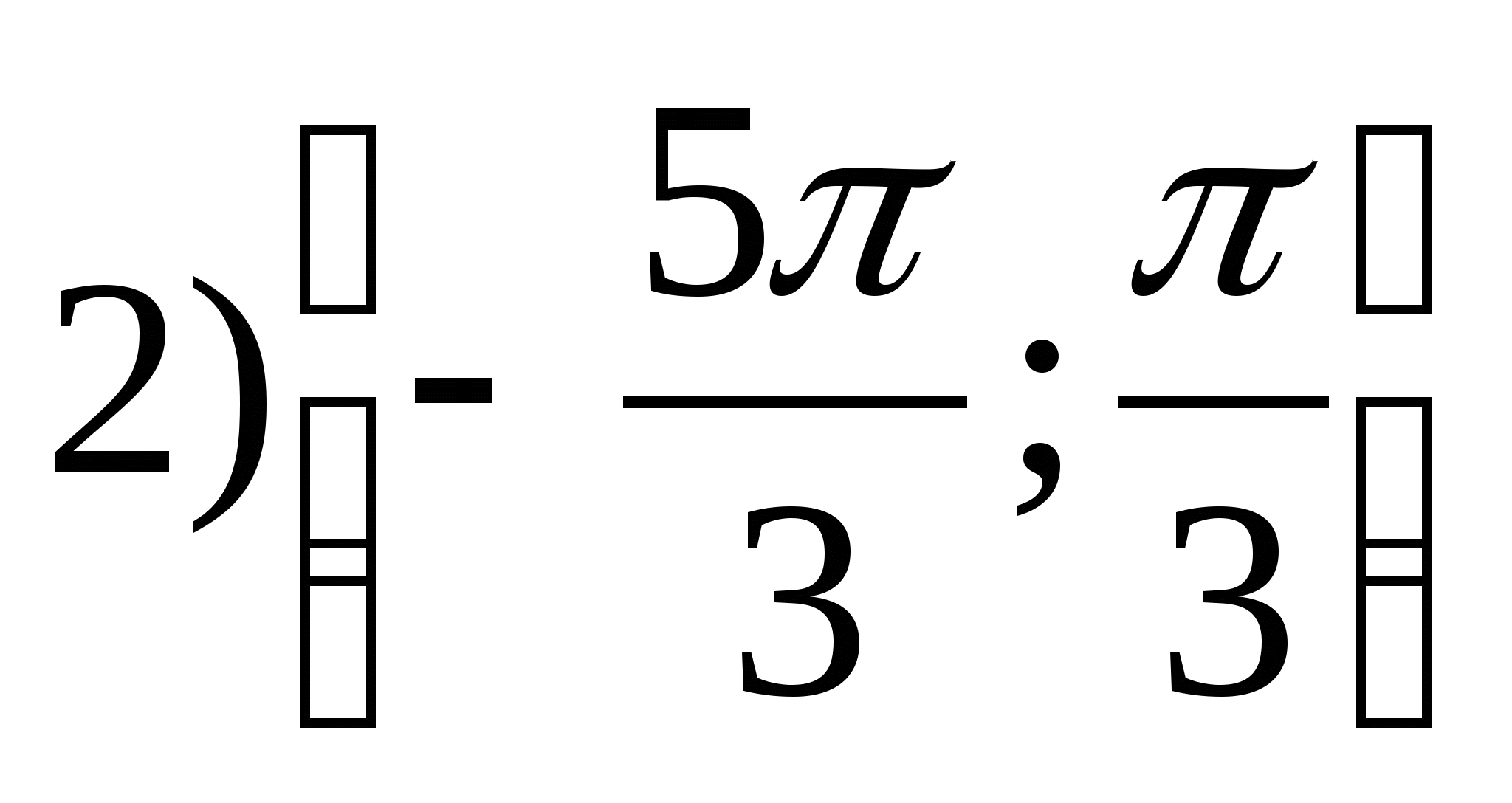
2. Find the smallest value of the function

1) 3,5 2) 0 3) 2,5 4) -3,5

3. Which of the following numbers can be the value of the function

1) -4 2) -1 3) 3 4) 7

4. At what values of the parameterm the equation cos (3 x + 2)- m= 5 has roots?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. Find the set of function values \u200b\u200by \u003d -2ctg 2 3 x + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. Specify the largest value of the function
in between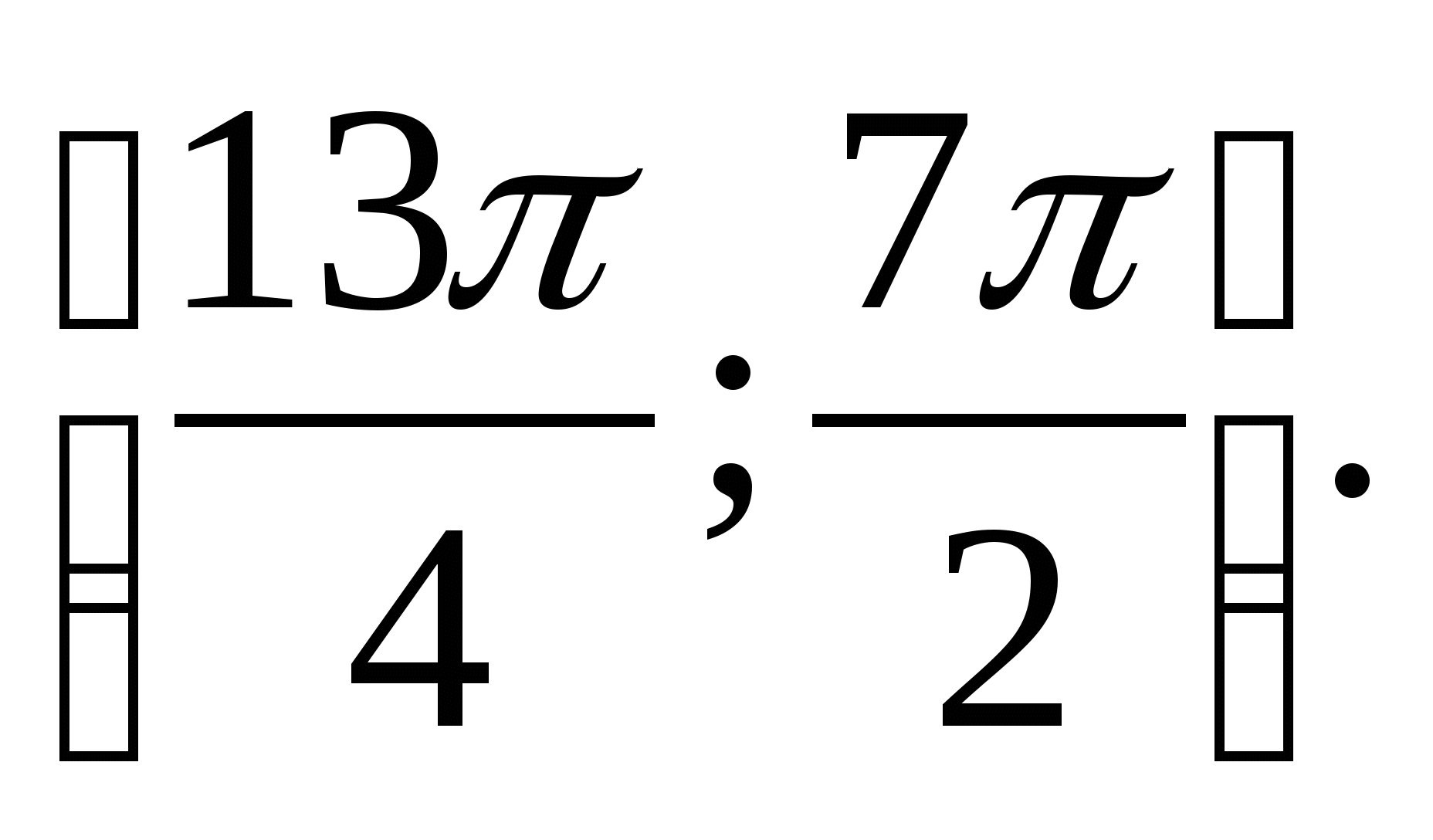

2) 0 3) 2 4) 1

7. Find how many integers are in the range of the function

1) 30 2) 35 3) 17 4) 7

Set of values of exponential and logarithmic functions

Option 1

1. Find the range of the function

1) 4) (-∞;3)

2. Specify a set of function values

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

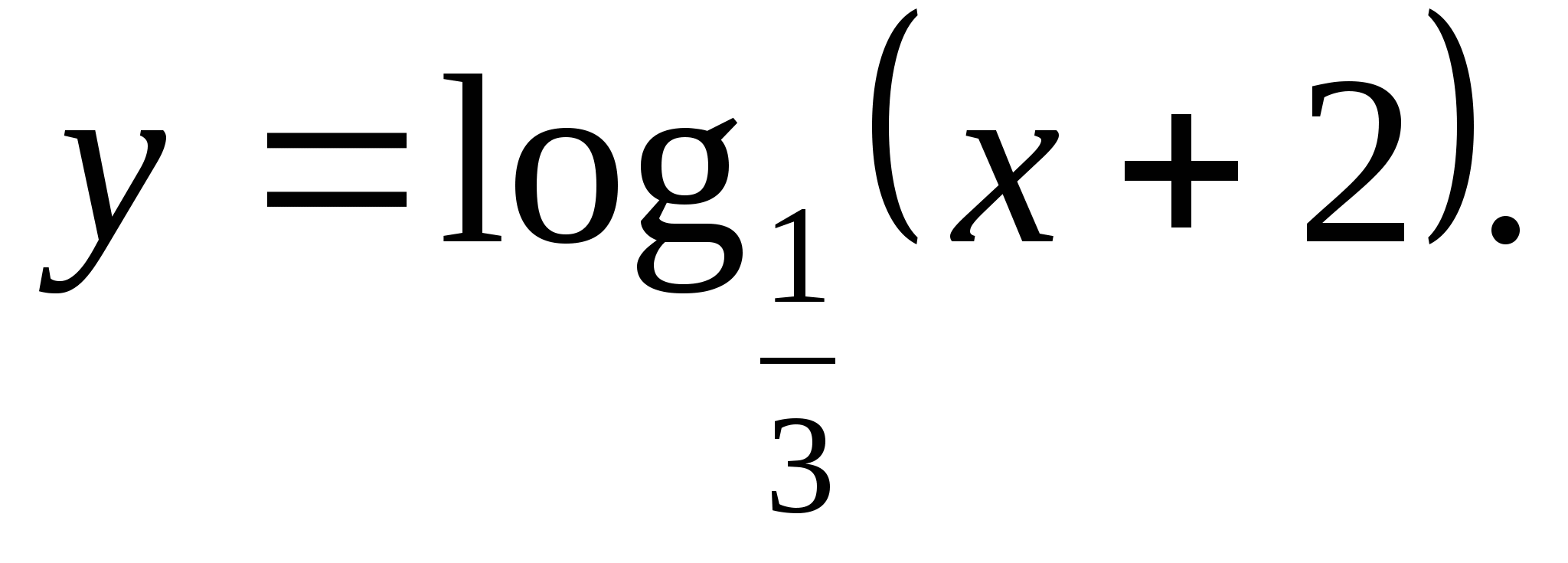
1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. Specify the smallest integer value of the function

1) 1 2) -1 3) 0 4) -5

7. Specify a function whose set of values is the interval (1;∞).

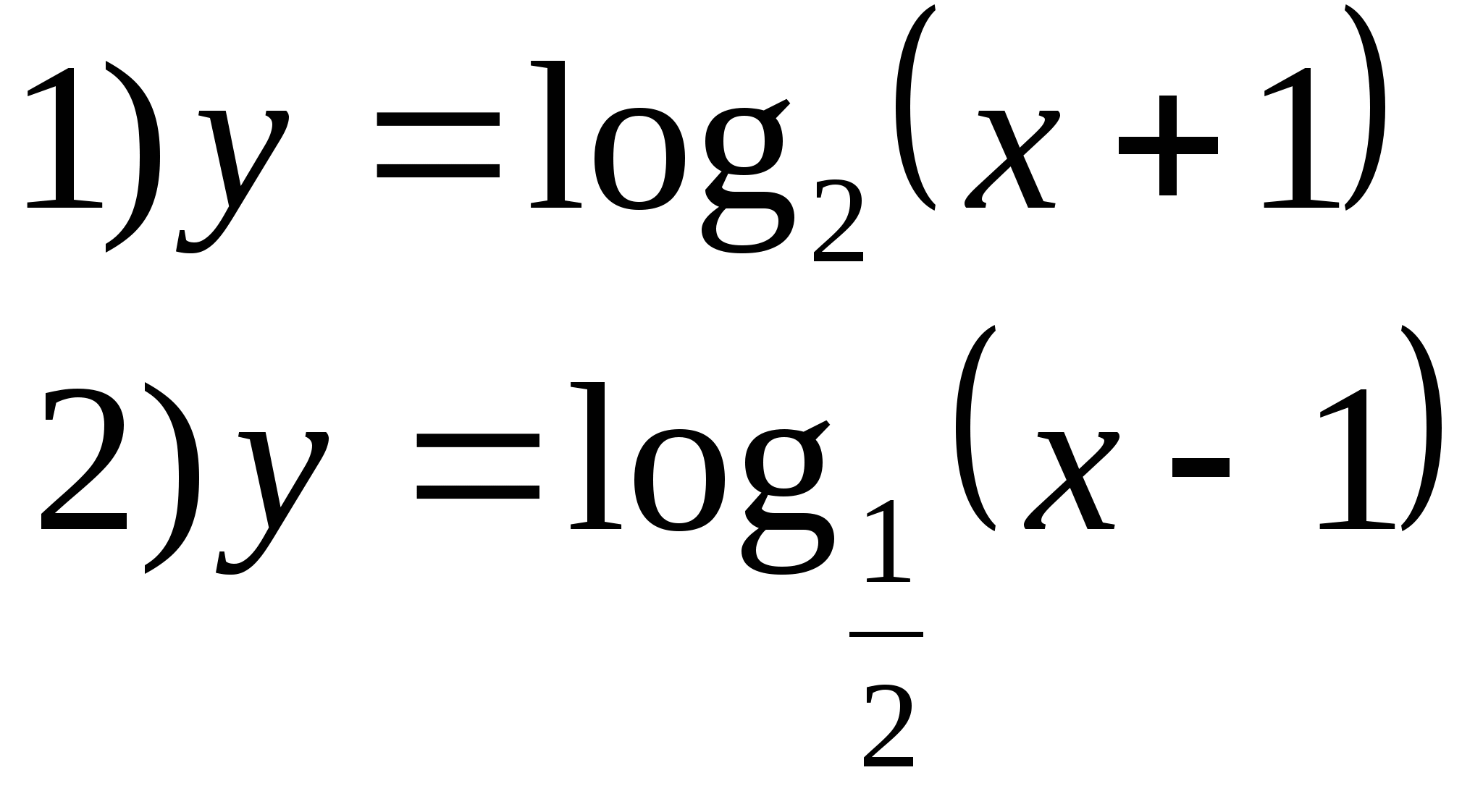
Option 2

1. Specify a set of function values

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. Find the range of the function

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. Specify the smallest integer value of the function

1) -12 2) -11 3) -10 4) -15

4. Specify a number that does not belong to the set of function values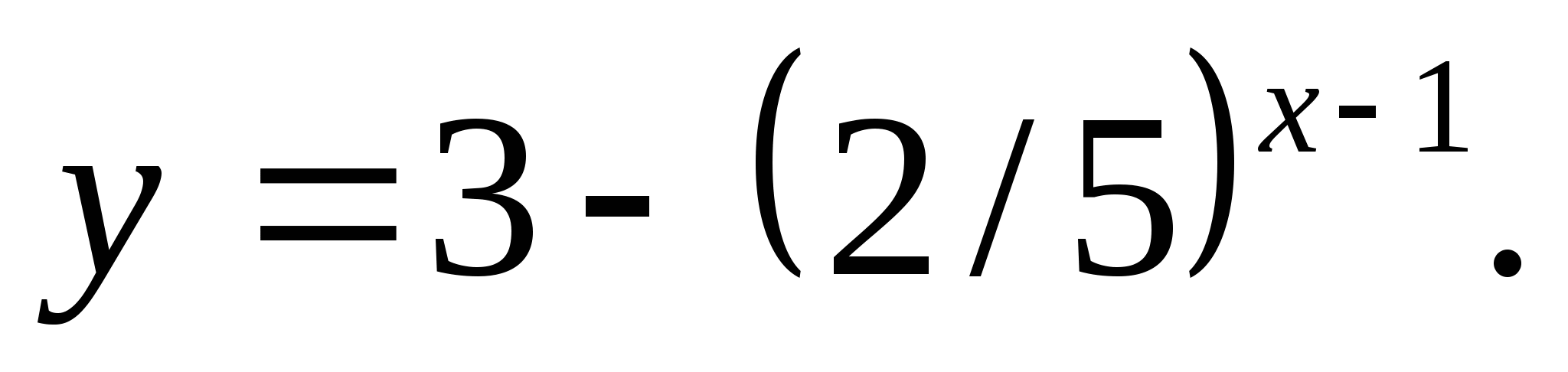

1) -42 2) 3 3) 1 4) -20

5. Specify a set of function values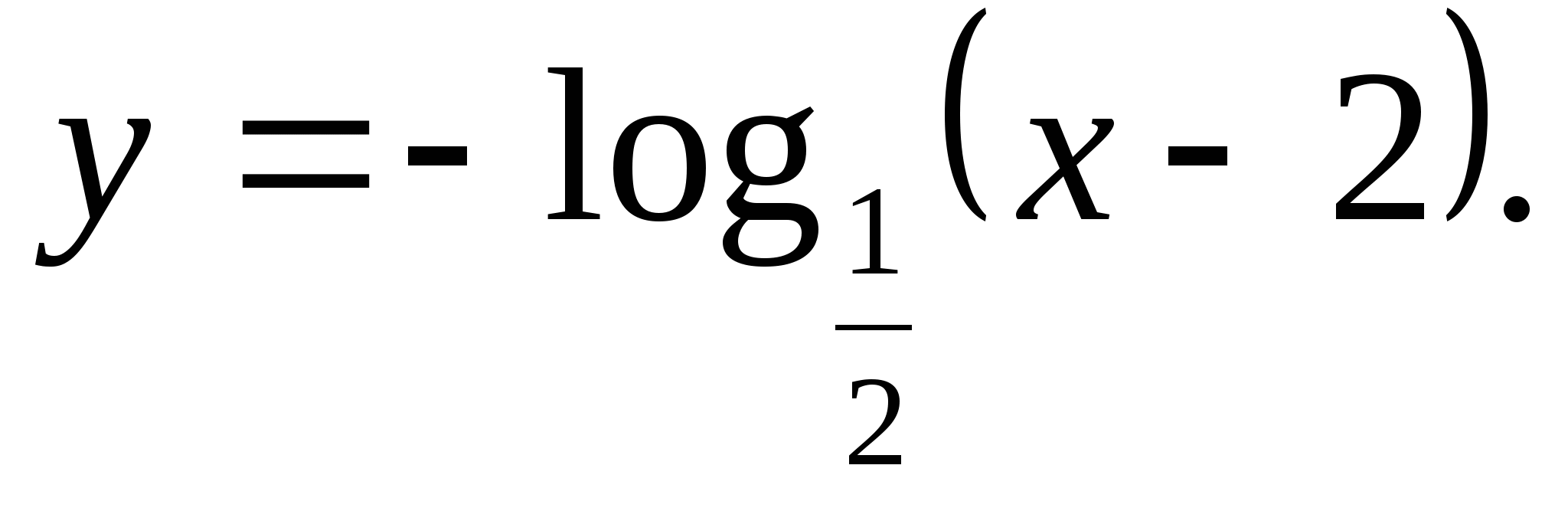

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. Specify the largest integer value of the function

1) 10 2) 3 3) 9 4) 2

7. Specify a function whose set of values is the interval

(-∞;13).

Option 5

1. Specify the smallest integer value of the function

1) 0 2) -1 3) -2 4) -3

2. Which of the following numbers is in the range of the function

1) -3 2) -4 3) 5 4) 0

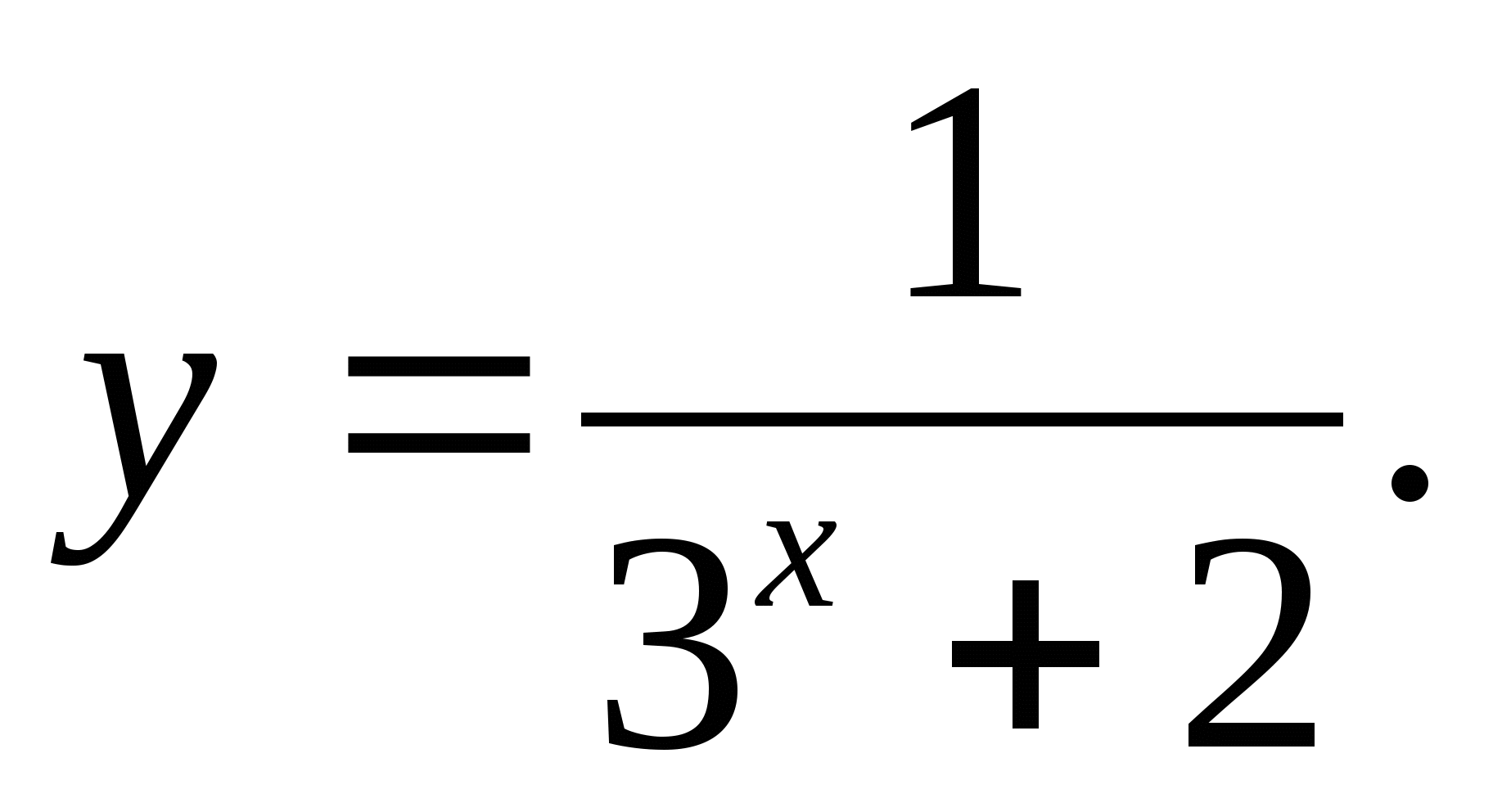
1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. Find on which segment the function
takes on the largest value of 2 and the smallest value of -3.

1) 2) (-5;2) 3) 4) (-3;2)

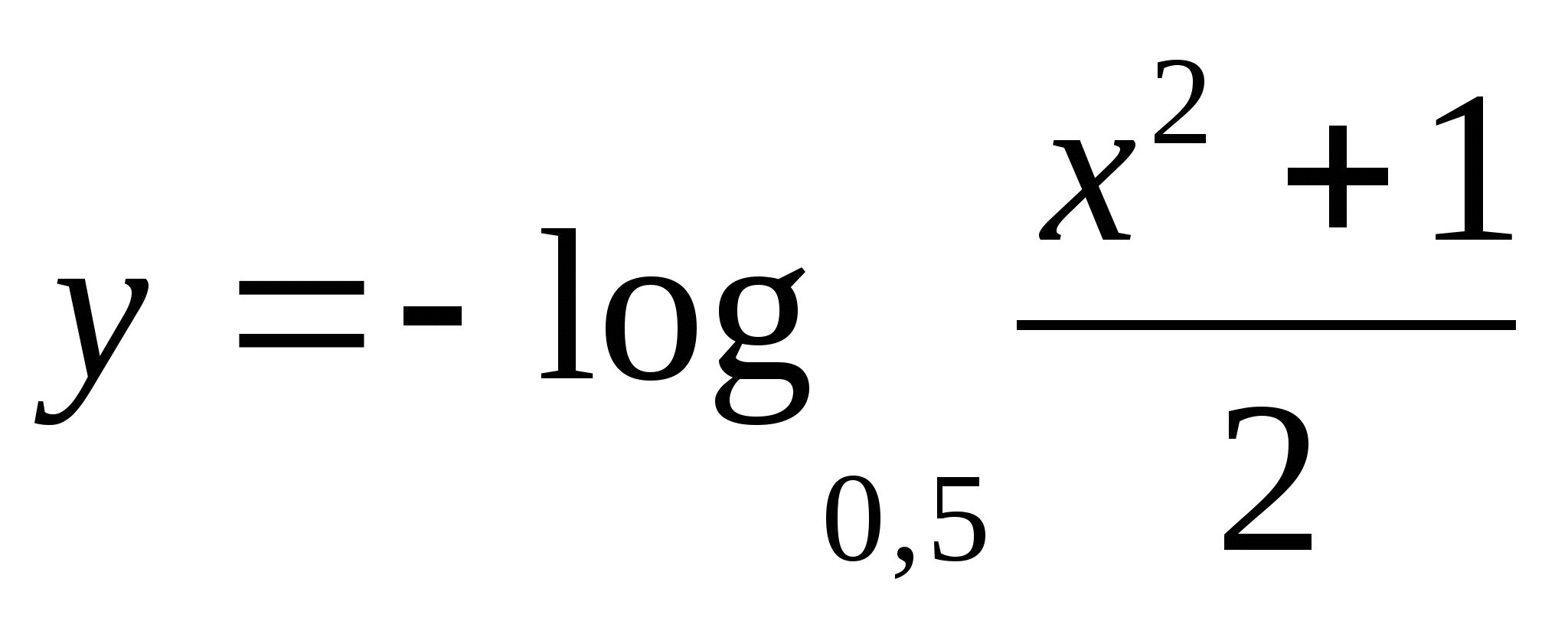in between

1) -1/2 2) 5 3) 2 4) 4

8. Find the sum of all natural numbers not included in the value sets of the function

1) 3 2) 6 3) 10 4) 8

Option 6

1. Specify the largest integer value of the function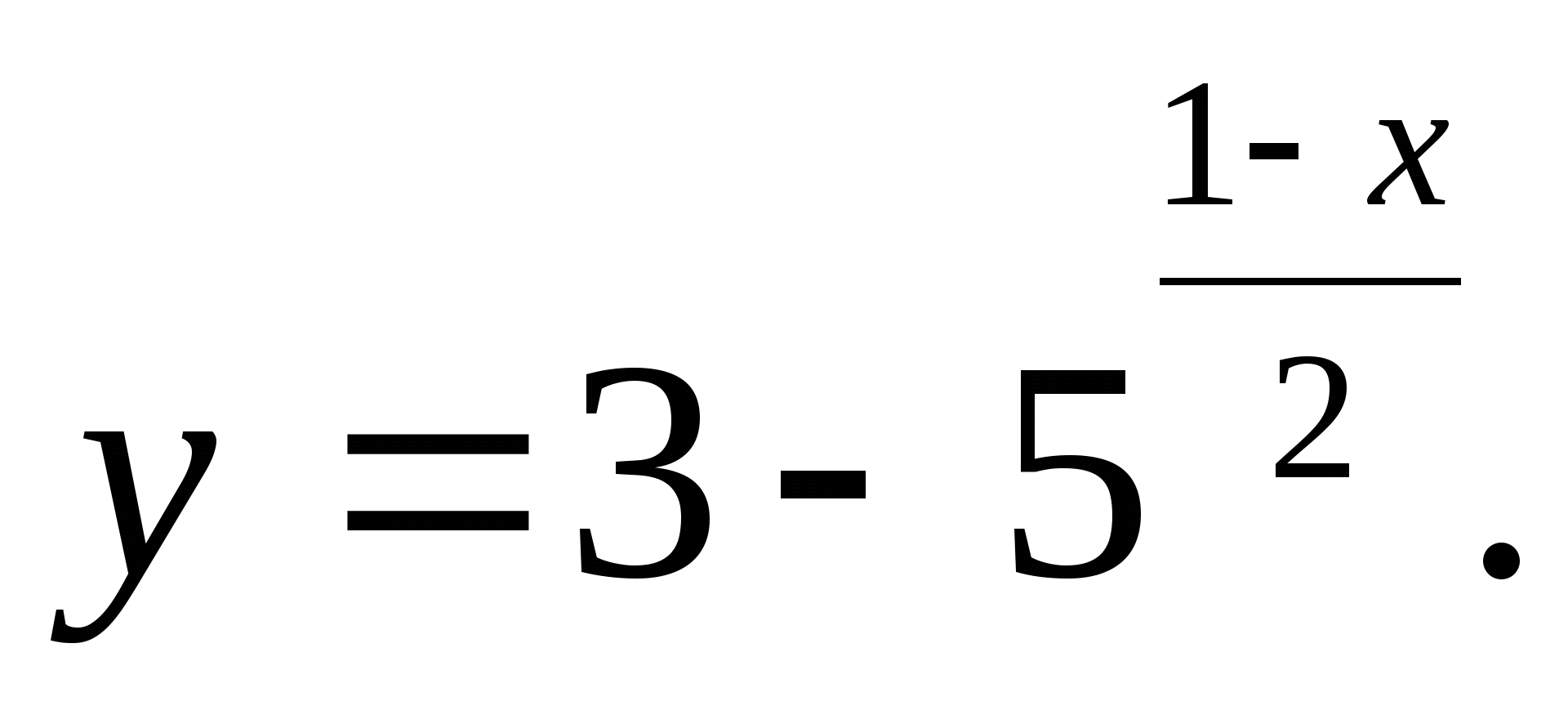

1) 2 2) 4 3) 3 4) 5

2. Which of the following numbers is not in the range of the function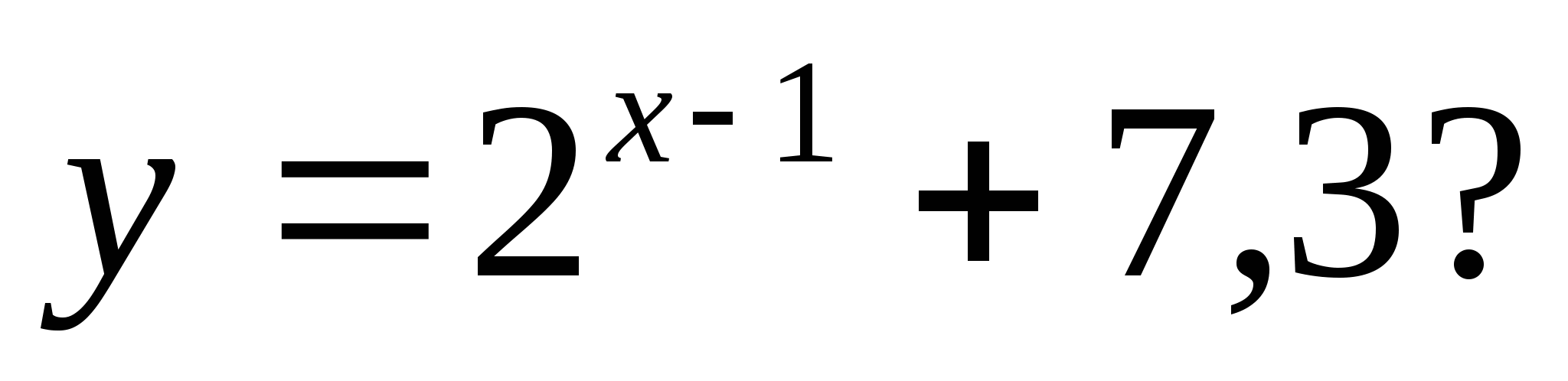

1) 35 2) 7, 28 3) 7, 85 4) 128

3. Specify a set of function values

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. Find all points on the OU that are projections of the points of the graph of the function

1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)

6. Find on which segment the function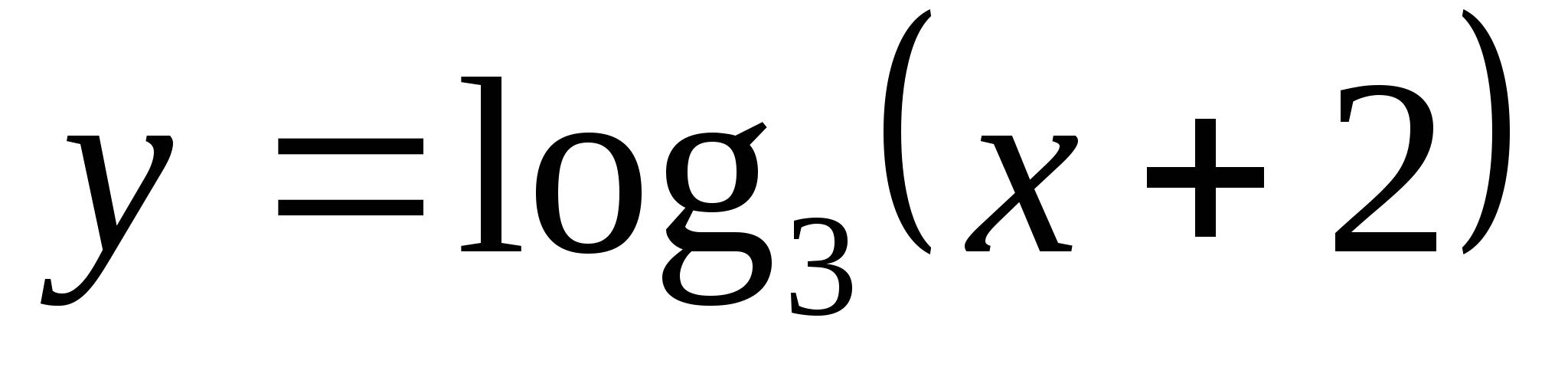
takes the smallest value as -2 and the largest value as 4.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. Specify the largest value of the function
in between

[-0.9; 0]. 2. Find the smallest value of the function on the segment.

4. How many integer values does the function take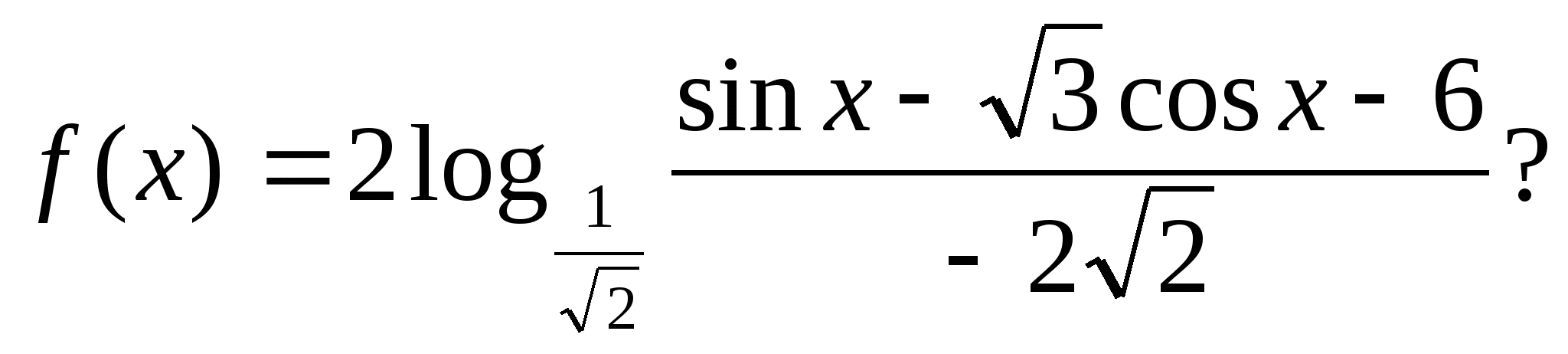

Answers

Part 1

Set of exponential and logarithmic function values

Part 2

The concept of a function and everything connected with it is traditionally complex, not fully understood. A special stumbling block in the study of the function and preparation for the exam is the domain of definition and the range of values (changes) of the function.
Often, students do not see the difference between the domain of a function and the domain of its values.
And if students manage to master the tasks of finding the domain of definition of a function, then the tasks of finding a set of values of a function cause them considerable difficulties.
The purpose of this article: familiarization with the methods of finding the values of a function.
As a result of consideration of this topic, theoretical material was studied, methods for solving problems of finding sets of function values were considered, didactic material was selected for independent work of students.
This article can be used by a teacher when preparing students for final and entrance exams, when studying the topic “The scope of a function” in optional classes in elective courses in mathematics.

I. Determining the scope of the function.

The area (set) of values E(y) of the function y = f(x) is the set of such numbers y 0 , for each of which there is such a number x 0 that: f(x 0) = y 0 .

Let us recall the ranges of the main elementary functions.

Consider a table.

Function	Many values
y = kx + b	E(y) = (-∞;+∞)
y=x2n	E(y) =
y = cos x	E(y) = [-1;1]
y = tg x	E(y) = (-∞;+∞)
y = ctg x	E(y) = (-∞;+∞)
y = arcsin x	E(y) = [-π/2 ; π/2]
y = arcos x	E(y) =
y = arctan x	E(y) = (-π/2 ; π/2)
y = arcctg x	E(y) = (0; π)

Note also that the range of any polynomial of even degree is the interval , where n is the largest value of this polynomial.

II. Function properties used in finding the range of a function

To successfully find the set of values of a function, one must have a good knowledge of the properties of the basic elementary functions, especially their domains of definition, ranges of values, and the nature of monotonicity. Let us present the properties of continuous, monotone differentiable functions, which are most often used in finding the set of values of functions.

Properties 2 and 3 are usually used together with the property of an elementary function to be continuous in its domain. In this case, the simplest and shortest solution to the problem of finding the set of values of a function is achieved on the basis of property 1, if it is possible to determine the monotonicity of the function using simple methods. The solution of the problem is further simplified if the function, in addition, is even or odd, periodic, etc. Thus, when solving problems of finding sets of function values, the following properties of the function should be checked and used as necessary:

continuity;
monotone;
differentiability;
even, odd, periodic, etc.

Simple tasks for finding a set of function values are mostly oriented:

a) the use of the simplest estimates and restrictions: (2 x > 0, -1 ≤ sinx? 1, 0 ≤ cos 2 x? 1, etc.);

b) to select a full square: x 2 - 4x + 7 \u003d (x - 2) 2 + 3;

c) for the transformation of trigonometric expressions: 2sin 2 x - 3cos 2 x + 4 = 5sin 2 x +1;

d) using the monotonicity of the function x 1/3 + 2 x-1 increases by R.

III. Consider ways to find the ranges of functions.

a) sequential finding of values of complex function arguments;
b) assessment method;
c) using the properties of continuity and monotonicity of a function;
d) use of a derivative;
e) the use of the largest and smallest values of the function;
f) graphical method;
g) parameter introduction method;
h) inverse function method.

We will reveal the essence of these methods on specific examples.

Example 1: Find the range E(y) functions y = log 0.5 (4 - 2 3 x - 9 x).

Let's solve this example by sequentially finding the values of complex function arguments. Having selected the full square under the logarithm, we transform the function

y = log 0.5 (5 - (1 + 2 3 x - 3 2x)) = log 0.5 (5 - (3 x + 1) 2)

And sequentially find the sets of values of its complex arguments:

E(3 x) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2) = (-∞;4)

Denote t= 5 – (3 x +1) 2 , where -∞≤ t≤4. Thus, the problem is reduced to finding the set of values of the function y = log 0.5 t on the ray (-∞;4) . Since the function y = log 0.5 t is defined only at, then its set of values on the ray (-∞;4) coincides with the set of function values on the interval (0;4), which is the intersection of the ray (-∞;4) with domain of definition (0;+∞) of the logarithmic function. On the interval (0;4) this function is continuous and decreasing. At t> 0, it tends to +∞, and when t = 4 takes the value -2, so E(y) =(-2, +∞).

Example 2: Find the range of a function

y = cos7x + 5cosx

Let us solve this example by the method of estimates, the essence of which is to estimate the continuous function from below and from above and to prove that the function reaches the lower and upper bounds of the estimates. In this case, the coincidence of the set of values of the function with the interval from the lower bound of the estimate to the upper one is determined by the continuity of the function and the absence of other values for it.

From the inequalities -1≤cos7x?1, -5≤5cosx?5 we get the estimate -6≤y?6. For x = p and x = 0, the function takes the values -6 and 6, i.e. reaches the lower and upper bounds. As a linear combination of continuous functions cos7x and cosx, the function y is continuous along the entire number axis, therefore, by the property of a continuous function, it takes all values from -6 to 6 inclusive, and only them, since, due to the inequalities -6≤y?6, other values she is impossible. Hence, E(y)= [-6;6].

Example 3: Find the range E(f) functions f(x)= cos2x + 2cosx.

Using the double angle cosine formula, we transform the function f(x)= 2cos 2 x + 2cosx – 1 and denote t= cosx. Then f(x)= 2t 2 + 2t – 1. Since E(cosx) =

[-1;1], then the range of the function f(x) coincides with the set of values of the function g (t)\u003d 2t 2 + 2t - 1 on the segment [-1; 1], which we will find by a graphical method. Having plotted the function y = 2t 2 + 2t - 1 = 2(t + 0.5) 2 - 1.5 on the interval [-1; 1], we find E(f) = [-1,5; 3].

Note – Many problems with a parameter are reduced to finding the set of values of a function, mainly related to the solvability and the number of solutions of the equation and inequalities. For example, the equation f(x)= a is solvable if and only if

aE(f) Similarly, the equation f(x)= a has at least one root located on some interval X, or has no root on this interval if and only if a belongs or does not belong to the set of values of the function f(x) on the interval X. We also study using the set of values of the function and the inequalities f(x)≠ a, f(x)> a etc. In particular, f(x)≠ and for all admissible values of x, if a E(f)

Example 4. For what values of the parameter a, the equation (x + 5) 1/2 = a (x 2 + 4) has a single root on the segment [-4;-1].

Let's write the equation in the form (x + 5) 1/2 / (x 2 + 4) = a. The last equation has at least one root on the segment [-4;-1] if and only if a belongs to the set of values of the function f(x) =(x + 5) 1/2 / (x 2 + 4) on the segment [-4;-1]. Let's find this set using the property of continuity and monotonicity of the function.

On the segment [-4;-1] the function y = xІ + 4 is continuous, decreasing and positive, therefore the function g(x) = 1/(x 2 + 4) is continuous and increases on this interval, since when dividing by a positive function, the nature of the monotonicity of the function changes to the opposite. Function h(x) =(x + 5) 1/2 is continuous and increasing in its domain D(h) =[-5;+∞) and, in particular, on the interval [-4;-1], where it is also positive. Then the function f(x)=g(x) h(x), as a product of two continuous, increasing and positive functions, is also continuous and increases on the segment [-4;-1], therefore its set of values on [-4;-1] is the segment [ f(-4); f(-1)] = . Therefore, the equation has a solution on the interval [-4;-1], and the only one (by the property of a continuous monotone function), for 0.05 ≤ a ≤ 0.4

Comment. Solvability of the equation f(x) = a on some interval X is equivalent to belonging of the values of the parameter a set of function values f(x) on X. Therefore, the set of values of the function f(x) on the interval X coincides with the set of parameter values a, for which the equation f(x) = a has at least one root on the interval X. In particular, the range of values E(f) functions f(x) matches the set of parameter values a, for which the equation f(x) = a has at least one root.

Example 5: Find the range E(f) functions

Let's solve the example by introducing a parameter, according to which E(f) matches the set of parameter values a, for which the equation

has at least one root.

When a=2, the equation is linear - 4x - 5 = 0 with a non-zero coefficient for unknown x, therefore it has a solution. For a≠2, the equation is quadratic, so it is solvable if and only if its discriminant

Since the point a = 2 belongs to the segment

then the desired set of parameter values a, hence the range of values E(f) will be the entire segment.

As a direct development of the method of introducing a parameter when finding a set of values of a function, we can consider the method of the inverse function, to find which it is necessary to solve the equation for x f(x)=y, considering y as a parameter. If this equation has a unique solution x=g(y), then the range E(f) original function f(x) coincides with the domain of definition D(g) inverse function g(y). If the equation f(x)=y has multiple solutions x = g 1 (y), x \u003d g 2 (y) etc., then E(f) is equal to the union of the scopes of the function definitions g 1 (y), g 2 (y) etc.

Example 6: Find the range E(y) functions y = 5 2/(1-3x).

From the equation

find the inverse function x = log 3 ((log 5 y – 2)/(log 5 y)) and its domain D(x):

Since the equation for x has a unique solution, then

E(y) = D(x) = (0; 1)(25;+∞ ).

If the domain of a function consists of several intervals or the function on different intervals is given by different formulas, then to find the domain of the function, you need to find the sets of values of the function on each interval and take their union.

Example 7: Find ranges f(x) and f(f(x)), where

f(x) on the ray (-∞;1], where it coincides with the expression 4 x + 9 4 -x + 3. Denote t = 4 x. Then f(x) = t + 9/t + 3, where 0< t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f(x) on the ray (-∞;1] coincides with the set of values of the function g(t) = t + 9/t + 3, on the interval (0;4], which we find using the derivative g'(t) \u003d 1 - 9 / t 2. On the interval (0;4] the derivative g'(t) is defined and vanishes there at t=3. At 0<t<3 она отрицательна, а при 3<t<4 положительна. Следовательно, в интервале (0;3) функция g(t) decreases, and in the interval (3;4) it increases, remaining continuous on the entire interval (0;4), so g (3)= 9 - the smallest value of this function on the interval (0; 4], while its largest value does not exist, so when t→0 right function g(t)→+∞. Then, by the property of a continuous function, the set of values of the function g(t) on the interval (0;4], and hence the set of values f(x) on (-∞;-1], there will be a ray .

Now, by combining the intervals - the sets of function values f(f(x)), denote t = f(x). Then f(f(x)) = f(t), where t function f(t)= 2cos( x-1) 1/2+ 7 and it again takes all values from 5 to 9 inclusive, i.e. range E(fІ) = E(f(f(x))) =.

Similarly, denoting z = f(f(x)), you can find the range E(f3) functions f(f(f(x))) = f(z), where 5 ≤ z ≤ 9, etc. Make sure that E(f 3) = .

The most universal method for finding the set of function values is to use the largest and smallest values of the function in a given interval.

Example 8. For what values of the parameter R inequality 8 x - p ≠ 2x+1 – 2x holds for all -1 ≤ x< 2.

Denoting t = 2 x, we write the inequality as p ≠ t 3 - 2t 2 + t. Because t = 2 x is a continuously increasing function on R, then for -1 ≤ x< 2 переменная

2 -1 ≤ t<2 2 ↔

0.5 ≤ t< 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда R different from function values f(t) \u003d t 3 - 2t 2 + t at 0.5 ≤ t< 4.

Let us first find the set of values of the function f(t) on the interval where it has a derivative everywhere f'(t) = 3t 2 - 4t + 1. Hence, f(t) is differentiable, and therefore continuous on the segment . From the equation f'(t) = 0 find the critical points of the function t=1/3, t=1, the first of which does not belong to the segment , and the second belongs to it. Because f(0.5) = 1/8, f(1) = 0, f(4) = 36, then, by the property of a differentiable function, 0 is the smallest, and 36 is the largest value of the function f(t) on the segment. Then f(t), as a continuous function, takes on the segment all values from 0 to 36 inclusive, and the value 36 takes only when t=4, so for 0.5 ≤ t< 4, она принимает все значения из промежутка $y = (\rmtg)\, x$E(y) = (-∞;+∞) $y = (\rm ctg)\, x$E(y) = (-∞;+∞) $y = \arcsin(x)$E(y) = [-π/2; π/2] $y = \arccos(x)$E(y) = $y = (\rm arctg)\, x$E(y) = (-π/2; π/2) $y = (\rm arcctg)\, x$E(y) = (0; π)

Examples

Find the set of function values:

Using the derivative

Find the domain of definition: D(f)=[-3;3], because $9-x^(2)\geq 0$

Find the derivative: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$

f"(x) = 0 if x = 0. f"(x) does not exist if $\sqrt(9-x^(2))=0$ i.e. for x = ±3. We get three critical points: x 1 \u003d -3, x 2 \u003d 0, x 3 \u003d 3, two of which coincide with the ends of the segment. Calculate: f(–3) = 0, f(0) = 3, f(3) = 0. Thus, the smallest value of f(x) is 0, the largest value is 3.

Answer: E(f) = .

NOT using derivative

Find the largest and smallest values of the function:

Since $
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ , then:

$f(x)\leq \frac(3)(4)$ for all x;

$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ for all x(because $|\cos (x)|\leq 1$);

$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;

$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;

Answer: $\frac(3)(4)$ and $-\frac(3)(2)$

If you solve this problem with the help of derivatives, then you will need to overcome the obstacles associated with the fact that the function f (x) is defined not on a segment, but on the entire real line.

Using the bounds/estimates method

It follows from the definition of sine that $-1\leq\sin(x)\leq 1$. Next, we use the properties of numerical inequalities.

$-4\leq - 4\sin(x)\leq 4$, (multiply all three parts of the double inequality by -4);

$1\leq 5 - 4\sin(x)\leq 9$ (added to the three parts of the double inequality 5);

Since this function is continuous over the entire domain of definition, the set of its values lies between its smallest and largest value over the entire domain of definition, if any.

In this case, the set of values of the function $y = 5 - 4\sin(x)$ is the set .

From the inequalities $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ we obtain the estimate $$\\ -6\leq y\leq 6$ $

For x = p and x = 0, the function takes the values -6 and 6, i.e. reaches the lower and upper bounds. As a linear combination of cos(7x) and cos(x) continuous functions, the y function is continuous along the entire number axis, so by the property of a continuous function it takes all values from -6 to 6 inclusive, and only them, since due to the inequalities $- 6\leq y\leq 6$ other values are impossible for it.

Therefore, E(y) = [-6;6].

$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Answer: E(f) = .

$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].

$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .

Let us transform the expression $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ((\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)(2)) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac(\pi) (4)) $$.

The definition of cosine implies $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$

Since this function is continuous on the entire domain of definition, then the set of its values is enclosed between its smallest and largest value, if any, the set of values of the function $y =\sqrt(2)\cos((x +\frac(\pi)(4 )))$ is the set $[-\sqrt(2);\sqrt(2)]$.

$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$

Denote $t = 5 – (3^(x)+1)^(2)$, where -∞≤t≤4. Thus, the problem is reduced to finding the set of values of the function $y = \log_(0,5)(t)$ on the ray (-∞;4). Since the function $y = \log_(0,5)(t)$ is defined only for t > 0 , its set of values on the ray (-∞;4) coincides with the set of values of the function on the interval (0;4) representing is the intersection of the ray (-∞;4) with the domain of definition (0;+∞) of the logarithmic function. On the interval (0;4) this function is continuous and decreasing. For t > 0, it tends to +∞, and for t = 4 it takes on the value -2, so E(y) = (-2, +∞).

We use a technique based on a graphic representation of a function.

After transformations of the function, we have: y 2 + x 2 = 25, and y ≥ 0, |x| ≤ 5.

It should be recalled that $x^(2)+y^(2)=r^(2)$ is the equation of a circle of radius r.

Under these restrictions, the graph of this equation is the upper semicircle centered at the origin and radius equal to 5. It is obvious that E(y) = .

Answer: E(y) = .